【题目】(本题有两道题,请从(1)、(2)题中选一题作答即可)
(1)某品牌太阳镜由一个镜架和两个镜片配套构成,每个工人每天可以加工![]() 个镜架或者加工
个镜架或者加工![]() 个镜片,现有
个镜片,现有![]() 名工人,应怎么安排人力,才能使每天生产的镜架和镜片配套?能做成多少副太阳镜?
名工人,应怎么安排人力,才能使每天生产的镜架和镜片配套?能做成多少副太阳镜?
(2)去年春季,蔬菜种植场在![]() 公顷的大棚地里分别种植了茄子和西红柿,总费用是
公顷的大棚地里分别种植了茄子和西红柿,总费用是![]() 万元.其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
万元.其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
每公顷费用 万元 | 每公顷获利 万元 | |
茄子 |
|
|
西红柿 |
|
|
请解答下列问题:
①求出茄子和西红柿的种植面积各为多少公顷?
②种植场在这一季共获利多少万元?
参考答案:
【答案】(1) 有40人生产镜加,20人生产镜片;每天能做4000副;(2) ①茄子种植5公顷,西红柿种植10公顷;②这一季共获利38万元.
【解析】
(1)设有![]() 人生产镜架,
人生产镜架,![]() 人生产镜片,由题意列出二元一次方程组即可求解;
人生产镜片,由题意列出二元一次方程组即可求解;
(2)设匣子种植![]() 公顷,西红柿种植
公顷,西红柿种植![]() 公顷,由题意列出二元一次方程组即可求解.
公顷,由题意列出二元一次方程组即可求解.
(1)解:设有![]() 人生产镜架,
人生产镜架,![]() 人生产镜片,由题意得:
人生产镜片,由题意得:
![]()
解之得:![]()
经检验,符合题意.
![]() (副)
(副)
答:有![]() 人生产镜加,
人生产镜加,![]() 人生产镜片;每天能做
人生产镜片;每天能做![]() 副 .
副 .
(2)解:设匣子种植![]() 公顷,西红柿种植
公顷,西红柿种植![]() 公顷,由题意得:
公顷,由题意得:
![]()
解之得:![]()
经检验,符合题意.
![]() (万元)
(万元)
答:①茄子种植![]() 公顷,西红柿种植
公顷,西红柿种植![]() 公顷②这一季共获利
公顷②这一季共获利![]() 万元.
万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0),B(1,0),直线x=-0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当-2<x<1时,y>0;③四边形ACBD是菱形;④9a-3b+c>0,你认为其中正确的是( )

A. ②③④B. ①②④C. ①③④D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
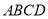 ,点
,点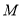 是线段
是线段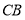 延长线一点,连结
延长线一点,连结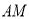 ,
,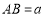 ,
,
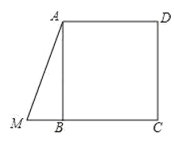
(1)将线段
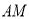 沿着射线
沿着射线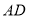 运动,使得点
运动,使得点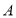 与点
与点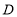 重合,用代数式表示线段
重合,用代数式表示线段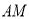 扫过的平面部分的面积.
扫过的平面部分的面积.(2)将三角形
 绕着点
绕着点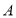 旋转,使得
旋转,使得 与
与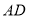 重合,点
重合,点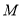 落在点
落在点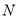 ,用代数式表示线段
,用代数式表示线段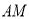 扫过的平面部分的面积.
扫过的平面部分的面积.(3)将三角形
 顺时针旋转,使旋转后的三角形有一边与正方形的一边完全重合(第(2)小题的情况除外),请在如图中画出符合条件的3种情况,并写出相应的旋转中心和旋转角
顺时针旋转,使旋转后的三角形有一边与正方形的一边完全重合(第(2)小题的情况除外),请在如图中画出符合条件的3种情况,并写出相应的旋转中心和旋转角 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,
 ,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:① ∠AED=∠CED;② OE=OD;③ BH=HF;④ BC-CF=2HE;⑤ AB=HF,其中正确的有( )
,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:① ∠AED=∠CED;② OE=OD;③ BH=HF;④ BC-CF=2HE;⑤ AB=HF,其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】 (用如图所示的曲尺形框框(有三个方向),可以套住下表中的三个数,设被框住的三个数中(第一个框框住的最小的数为a、第二个框框住的最小的数为b、第三个框框住的最小的数为c).
(1)第一个框框住的三个数中最小的数为a,三个数的和是: ;第二个框框住的三个数中最小的数为b,三个数的和是: ;第三个框框住的三个数中最小的数为c,三个数的和是: ;
(2)这三个框框住的数的和能是48吗?,能,求出最小的数a、b、c的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD为矩形,
 ,
, ,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,设运动时间为t秒.
,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,设运动时间为t秒.
(1)当点P在线段AB上运动了t秒时,
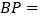 __________________(用代数式表示);
__________________(用代数式表示);(2)t为何值时,四边形PDEB是平行四边形:
(3)在直线AB上是否存在点Q,使以D、E、Q、P四点为顶点的四边形是菱形?若存在,求出t的值:若不存在,说明理由.
相关试题

