Question

【题目】如图①，在△ABC中，∠BAC=90°，AB=AC，点E在AC上（且不与点A，C重合），在△ABC的外部作△CED，使∠CED=90°，DE=CE，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．

（1）请直接写出线段AF，AE的数量关系 ；

（2）将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；

（3）在图②的基础上，将△CED绕点C继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．

Answer 1

【答案】(1)AF=AE；（2）AF=AE，证明详见解析；（3）结论不变，AF=AE，理由详见解析.

【解析】试题分析：（1）如图①中，结论：AF=AE，只要证明△AEF是等腰直角三角形即可．（2）如图②中，结论：AF=AE，连接EF，DF交BC于K，先证明△EKF≌△EDA再证明△AEF是等腰直角三角形即可．（3）如图③中，结论不变，AF=AE，连接EF，延长FD交AC于K，先证明△EDF≌△ECA，再证明△AEF是等腰直角三角形即可．

试题解析：（1）如图①中，结论：AF=AE．

理由：∵四边形ABFD是平行四边形，

∴AB=DF，

∵AB=AC，

∴AC=DF，

∵DE=EC，

∴AE=EF，

∵∠DEC=∠AEF=90°，

∴△AEF是等腰直角三角形，

∴AF=AE．

（2）如图②中，结论：AF=AE．

理由：连接EF，DF交BC于K．

∵四边形ABFD是平行四边形，

∴AB∥DF，

∴∠DKE=∠ABC=45°，

∴EKF=180°﹣∠DKE=135°，

∵∠ADE=180°﹣∠EDC=180°﹣45°=135°，

∴∠EKF=∠ADE，

∵∠DKC=∠C，

∴DK=DC，

∵DF=AB=AC，

∴KF=AD，

在△EKF和△EDA中，

，

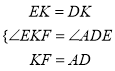∴△EKF≌△EDA，

∴EF=EA，∠KEF=∠AED，

∴∠FEA=∠BED=90°，

∴△AEF是等腰直角三角形，

∴AF=AE．

（3）如图③中，结论不变，AF=AE．

理由：连接EF，延长FD交AC于K．

∵∠EDF=180°﹣∠KDC﹣∠EDC=135°﹣∠KDC，

∠ACE=（90°﹣∠KDC）+∠DCE=135°﹣∠KDC，

∴∠EDF=∠ACE，

∵DF=AB，AB=AC，

∴DF=AC

在△EDF和△ECA中，

，

∴△EDF≌△ECA，

∴EF=EA，∠FED=∠AEC，

∴∠FEA=∠DEC=90°，

∴△AEF是等腰直角三角形，

∴AF=AE．