【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】首先根据折叠可得CD=AC=3,BC=4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,然后求得△BCF是等腰直角三角形,进而求得∠B/GD=90°,CE-EF=![]() ,ED=AE=
,ED=AE=![]() ,
,
从而求得B/D=1,DF=![]() ,在Rt△B/DF中,由勾股定理即可求得B/F的长.
,在Rt△B/DF中,由勾股定理即可求得B/F的长.
解:根据首先根据折叠可得CD=AC=3,B/C=B4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,
∴BD=4-3=1,∠DCE+∠B/CF=∠ACE+∠BCF,
∴∠ACB=90°,∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B/FC=135°,
∴∠B/FD=90°,
∵S△ABC=![]() AC×BC=
AC×BC=![]() AB×CE,
AB×CE,
∴AC×BC=AB×CE,
∵根据勾股定理求得AB=5,
∴CE=![]() ,∴EF=
,∴EF=![]() ,ED=AE=
,ED=AE=![]() =
=![]()
∴DE=EF-ED=![]() ,
,
∴B/F=![]() =
=![]() .
.
故答案为: ![]()
“点睛”此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理的应用等,根据折叠的性质求得相等的角是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:
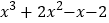 因式分解的结果为
因式分解的结果为 ,当
,当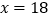 时,
时,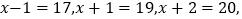 此时可以得到数字密码171920.
此时可以得到数字密码171920.(1)根据上述方法,当
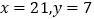 时,对于多项式
时,对于多项式 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式
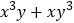 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);(3)若多项式
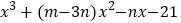 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当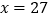 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】分类讨论是一种重要的数学方法,如在化简|a|时,可以这样分类:当a>0时,|a|=a;当a=0时,|a|=0;当a<0时,|a|=﹣a.用这种方法解决下列问题:
(1)当a=5时,求
 的值.
的值.(2)当a=﹣2时,求
 的值.
的值.(3)若有理数a不等于零,求
 的值.
的值.(4)若有理数a、b均不等于零,试求
 +
+ 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,池塘边有一块长为18m,宽为10m的长方形土地,现在将其 余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用整式表示:
(1)菜地的长a= m,宽b= m;
(2)菜地面积S= m2;
(3)当x=0.5m时,菜地面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们,我们很熟悉这样的算式:
 ,其实,数学不仅非常美妙,而且魅力无穷.请你欣赏下列一组等式:
,其实,数学不仅非常美妙,而且魅力无穷.请你欣赏下列一组等式:①

②

③

④

⑤……
(1)写出第⑤个等式:

(2)根据上述规律,写出第
 个等式:
个等式:
(3)观察比较,并大胆猜想:

(4)根据(2)的规律计算
 (写出计算过程)
(写出计算过程)
相关试题

