【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 , 其中正确结论是(填序号)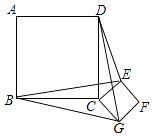
参考答案:
【答案】①②
【解析】解:设BE,DG交于O,
∵四边形ABCD和EFGC都为正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCE+∠DCE=∠ECG+∠DCE=90°+∠DCE,即∠BCE=∠DCG,
在△BCE和△DCG中,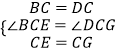 ,
,
∴△BCE≌△DCG(SAS),
∴BE=DG,
∴∠1=∠2,
∵∠1+∠4=∠3+∠1=90°,
∴∠2+∠3=90°,
∴∠BOC=90°,
∴BE⊥DG;故①②正确;
连接BD,EG,如图所示,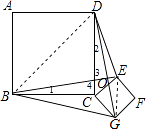
∴DO2+BO2=BD2=BC2+CD2=2a2 , EO2+OG2=EG2=CG2+CE2=2b2 ,
则BG2+DE2=DO2+BO2+EO2+OG2=2a2+2b2 , 故③错误.
所以答案是:①②.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某开发公司生产的 960 件新产品需要精加工后,才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用 20 天,而甲工厂每天加工的数量是乙工厂每天加工的数量的
 ,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家合作完成.在加工过程中,公司派一名工程师每天到厂进行技术指导,并负担每天 15 元的午餐补助费, 请你帮公司选择一种既省时又省钱的加工方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2﹣x+a=0有实根.
(1)求a的取值范围;
(2)设x1、x2是方程的两个实数根,且满足(x1+1)(x2+1)=﹣1,求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种货车,
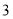 辆大货车与
辆大货车与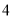 辆小火车一次可以运货
辆小火车一次可以运货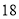 吨,
吨, 辆大货车与
辆大货车与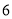 辆小货车一次可以运货
辆小货车一次可以运货 吨.
吨.(1)求
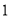 辆大货车和
辆大货车和 辆小货车一次可以分别运多少吨;
辆小货车一次可以分别运多少吨;(2)现有
 吨货物需要运输,货运公司拟安排大小货车共
吨货物需要运输,货运公司拟安排大小货车共 辆把全部货物一次运完.求至少需要安排几辆大货车?
辆把全部货物一次运完.求至少需要安排几辆大货车? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
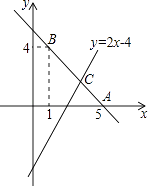
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_______度;
(2)如图2如果∠BAC=60°,则∠BCE=______度;
(3)设∠BAC=
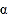 ,∠BCE=
,∠BCE=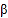 .
.①如图3,当点D在线段BC上移动,则
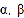 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,请直接写出
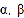 之样的数量关系,不用证明。
之样的数量关系,不用证明。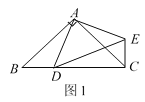

相关试题

