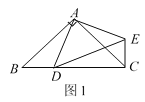
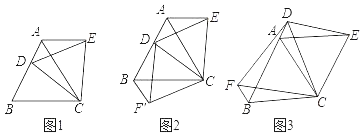
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_______度;
(2)如图2如果∠BAC=60°,则∠BCE=______度;
(3)设∠BAC=![]() ,∠BCE=
,∠BCE=![]() .
.
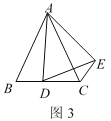
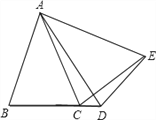
①如图3,当点D在线段BC上移动,则![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,请直接写出![]() 之样的数量关系,不用证明。
之样的数量关系,不用证明。

参考答案:
【答案】(1)90°(2)120° (3) ①α+β=180°②α+β=180°,α=β
【解析】
试题(1)由条件可证得△ABD≌△ACE,可得∠ABD=∠ACE=45°,利用条件可求得∠ACB=45°,可求得∠BCE=90°;
(2)同(1)可证得∠ABD=∠ACE,在△ABC中由等腰三角形的性质可求得∠ACD,从而可求得∠BCE;
(3)①同(1)可证得∠ABD=∠ACE,在△ABC中由等腰三角形的性质可求得∠ACD=∠ABC=![]() ,从而可求得∠BCE;②过程同①.
,从而可求得∠BCE;②过程同①.
试题解析:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中
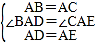
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,∠BAC=90°,
∴∠ABD=∠ACB=45°,
∴∠BCE=∠ACB+∠ACE=45°+45°=90°,
(2)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,∠BAC=60°,
∴∠ABD=∠ACB=![]() =60°,
=60°,
∴∠BCE=∠ACB+∠ACE=60°+60°=120°;
(3)①∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,∠BAC=α,
∴∠ABD=∠ACB=![]() ,
,
∴∠BCE=∠ACB+∠ACE=2∠ACB=180°-α,
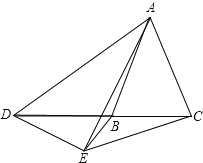
②如图,当点D在射线BC上时,α+β=180°
如图:当点D在射线BC的反向延长线上时,α=β.

-
科目: 来源: 题型:
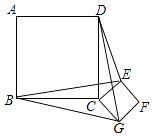
查看答案和解析>>【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 , 其中正确结论是(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
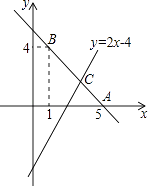
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校植物园沿路护栏的纹饰部分准备设计成若干个形状、大小完全相同的四边形图案,每平移一个图案,纹饰长度就增加
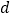 cm(如图)所示,已知每个四边形图案的水平方向的对角线长30cm.
cm(如图)所示,已知每个四边形图案的水平方向的对角线长30cm.(1)若
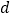 =26cm,且该纹饰要用231个四边形图案,求纹饰的长度
=26cm,且该纹饰要用231个四边形图案,求纹饰的长度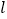 ;
;(2)当
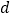 =20cm时,若保持(1)中纹饰长度不变,则需要多少个这样的四边形图案?
=20cm时,若保持(1)中纹饰长度不变,则需要多少个这样的四边形图案?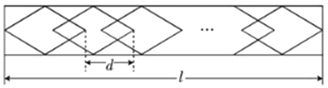
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=2
 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 .
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 . 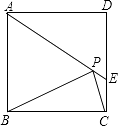
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,D是等边三角形ABC边BA上一动点(点D)与点B不重合,连接CD,以CD为边在BC上方作等边三角形DCE,连接AE,你能发现AE与BD之间的数量关系吗?并证明你发现的结论.
(2)如图二,当动点D在等边三角形ABC边BA上运动时(点D与点B不重合),连接DC,以DC为边在其上方、下方分别作等边三角形DCE和等边三角形DCF,连接AE,BF,探究AE,BF与AB有何数量关系?并证明你探究的结论.
(3)如图三,当动点D在等边三角形ABC边BA的延长线上运动时,其他作法与图2相同,若AE=8,BF=2,请直接写出AB= .
相关试题

