【题目】某开发公司生产的 960 件新产品需要精加工后,才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用 20 天,而甲工厂每天加工的数量是乙工厂每天加工的数量的![]() ,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
,公司需付甲工厂加工费用为每天 80 元,乙工厂加工费用为每天 120 元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家合作完成.在加工过程中,公司派一名工程师每天到厂进行技术指导,并负担每天 15 元的午餐补助费, 请你帮公司选择一种既省时又省钱的加工方案,并说明理由.
参考答案:
【答案】(1)甲工厂每天加工 16 件产品,乙工厂每天加工 24 件产品. (2)甲、乙两工厂合作完成此项任务既省时又省钱.见解析。
【解析】
(1)设甲工厂每天加工 x 件新品,乙工厂每天加工 1.5x 件新品,根据题意找出等量关系:甲厂单独加工这批产品所需天数﹣乙工厂单独加工完这批产品所需天数=20, 由等量关系列出方程求解.
(2)分别计算出甲单独加工完成、乙单独加工完成、甲、乙合作完成需要的时间和费用, 比较大小,选择既省时又省钱的加工方案即可.
(1)设甲工厂每天加工 x 件新品,乙工厂每天加工 1.5x 件新品,
则: ![]() 解得:x=16
解得:x=16
经检验,x=16 是原分式方程的解
∴甲工厂每天加工 16 件产品,乙工厂每天加工 24 件产品
(2)方案一:甲工厂单独完成此项任务,则需要的时间为:960÷16=60 天
需要的总费用为:60×(80+15)=5700 元
方案二:乙工厂单独完成此项任务,则
需要的时间为:960÷24=40 天
需要的总费用为:40×(120+15)=5400 元
方案三:甲、乙两工厂合作完成此项任务,设共需要 a 天完成任务,则
16a+24a=960
∴a=24
∴需要的总费用为:24×(80+120+15)=5 160 元
综上所述:甲、乙两工厂合作完成此项任务既省时又省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣2,﹣1),B(﹣4,1),C(﹣3,3).△ABC关于原点O对称的图形是△A1B1C1 .
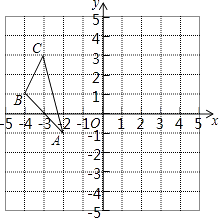
(1)画出△A1B1C1;
(2)BC与B1C1的位置关系是 , AA1的长为;
(3)若点P(a,b)是△ABC 一边上的任意一点,则点P经过上述变换后的对应点P1的坐标可表示为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:AD平分∠ABC.下面是部分推理过程,请你将其补充完整:
∵AD⊥BC于D,EG⊥BC(已知)
∴∠ADC=∠EGC=90°( )
∴EG∥AD( )
∴∠E=________( )、
∠1=__________( )
又∵∠E=∠1(已知)
∴∠2=∠3( )
∴AD平分∠BAC ( )
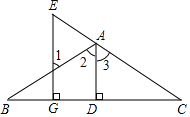
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2﹣x+a=0有实根.
(1)求a的取值范围;
(2)设x1、x2是方程的两个实数根,且满足(x1+1)(x2+1)=﹣1,求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种货车,
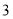 辆大货车与
辆大货车与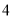 辆小火车一次可以运货
辆小火车一次可以运货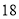 吨,
吨, 辆大货车与
辆大货车与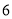 辆小货车一次可以运货
辆小货车一次可以运货 吨.
吨.(1)求
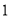 辆大货车和
辆大货车和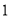 辆小货车一次可以分别运多少吨;
辆小货车一次可以分别运多少吨;(2)现有
 吨货物需要运输,货运公司拟安排大小货车共
吨货物需要运输,货运公司拟安排大小货车共 辆把全部货物一次运完.求至少需要安排几辆大货车?
辆把全部货物一次运完.求至少需要安排几辆大货车? -
科目: 来源: 题型:
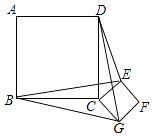
查看答案和解析>>【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 , 其中正确结论是(填序号)
相关试题

