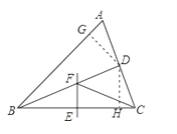
【题目】如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
(1)若∠A=60°,∠ABD=24°,求∠ACF的度数;
(2)若EF=4,BF:FD=5:3,S△BCF=10,求点D到AB的距离.

参考答案:
【答案】(1)48°;(2)![]()
【解析】试题分析:(1)先根据角平分线的性质, ∠ABD=24°,可求出∠ABC=2∠ABD=48°,再根据三角形内角和的定理可得: ∠ACB=72°,再根据垂直平分线的性质可求出∠FCB=∠DBC=24°,即可求解,(2)先过D作DG⊥AB于G,DH⊥BC于H,根据相似三角形的判定可判定△BEF∽△BHD,根据相似三角形的性质可得对应边成比例,可求出DH,即可求解.
试题解析:(1)∵BD平分∠ABC,∠ABD=24°,
∴∠ABC=2∠ABD=48°,∠DBC=∠ABD=24°,
∵∠A=60°,
∴∠ACB=180°﹣∠A﹣∠ACB=180°﹣60°﹣48°=72°,
∵FE是BC的中垂线,
∴FB=FC,
∴∠FCB=∠DBC=24°,
∴∠ACF=∠ACB﹣∠FCB=72°﹣24°=48°,
(2)过D作DG⊥AB于G,DH⊥BC于H,
∵BD平分∠ABC,
∴DG=DH,
∵EF⊥BC,
∴EF∥DH,
∴△BEF∽△BHD,
∴![]() ,
,
∵EF=4,BF:FD=5:3,
∴DH=![]() .
.
∴DG=DH=![]() ,
,
∴点D到AB的距离=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读材料,再尝试解决问题:
完全平方式
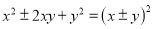 以及
以及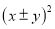 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求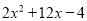 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:解:原式 =
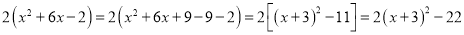 .
.因为无论
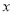 取什么数,都有
取什么数,都有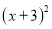 的值为非负数,所以
的值为非负数,所以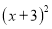 的最小值为0;此时
的最小值为0;此时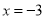 时,进而
时,进而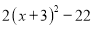 的最小值是
的最小值是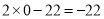 ;所以当
;所以当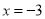 时,原多项式的最小值是
时,原多项式的最小值是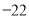 .
.请根据上面的解题思路,探求:
⑴.多项式
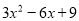 的最小值是多少,并写出对应的
的最小值是多少,并写出对应的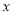 的取值;
的取值;⑵.多项式
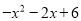 的最大值是多少,并写出对应的
的最大值是多少,并写出对应的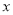 的取值.
的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列证明过程填空:
已知:如 图,AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2.
求证:AD平分∠BAC,填写证明中的空白.
证明:
∵AD⊥BC,EF⊥BC (已知),
∴EF∥AD ( ),
∴ = ( 两直线平行,内错角相等 ),
=∠CAD ( ).
∵ (已知),
∴ ,即AD平分∠BAC ( ).
-
科目: 来源: 题型:
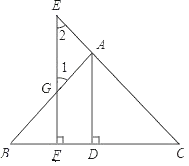
查看答案和解析>>【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)请你判断DA与CE的位置关系,并说明理由;
(2)若DA平分∠BDC,CE⊥AE于E,∠1=70°,试求∠FAB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在四边形ABCD中,
 ,延长BC至点E,连接AE交CD于点F,使
,延长BC至点E,连接AE交CD于点F,使
 求证:
求证:  ;
; 求证:
求证:  ;
; 若BF平分
若BF平分 ,请写出
,请写出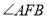 与
与 的数量关系______
的数量关系______ 不需证明
不需证明

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
∵
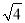 <
<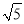 <
<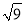 ,即2<
,即2<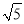 <3.
<3.∴
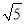 的整数部分为2,小数部分为
的整数部分为2,小数部分为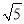 ﹣2,
﹣2,∴1<
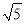 ﹣1<2
﹣1<2∴
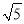 ﹣1的整数部分为1.
﹣1的整数部分为1.∴
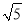 ﹣1的小数部分为
﹣1的小数部分为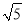 ﹣2
﹣2解决问题:已知:a是
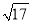 ﹣3的整数部分,b是
﹣3的整数部分,b是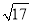 ﹣3的小数部分,
﹣3的小数部分,求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0)
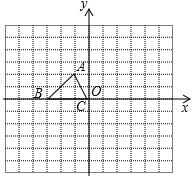
(1)请直接写出点A关于x轴对称的点
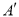 的坐标;
的坐标;(2)以C为位似中心,在x轴下方作△ABC的位似图形
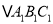 ,使放大前后位似比为1:2,请画出图形,并求出
,使放大前后位似比为1:2,请画出图形,并求出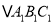 的面积.
的面积.
相关试题

