【题目】阅读理解
∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3.
<3.
∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ﹣2,
﹣2,
∴1<![]() ﹣1<2
﹣1<2
∴![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴![]() ﹣1的小数部分为
﹣1的小数部分为![]() ﹣2
﹣2
解决问题:已知:a是![]() ﹣3的整数部分,b是
﹣3的整数部分,b是![]() ﹣3的小数部分,
﹣3的小数部分,
求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
参考答案:
【答案】(1)a=1,b=![]() ﹣4;(2)±4.
﹣4;(2)±4.
【解析】试题分析:(1)先估算出![]() 的整数范围,再估算出
的整数范围,再估算出![]() -3的范围,即可求出a、b的值;(2)将a、b的值代入要求的式子,计算出结果即可.
-3的范围,即可求出a、b的值;(2)将a、b的值代入要求的式子,计算出结果即可.
试题解析:
解:(1)∵![]() <
<![]() <
<![]() ,
,
∴4<![]() <5,
<5,
∴1<![]() -3<2,
-3<2,
∴a=1,b=![]() -4;
-4;
(2)(-a)3+(b+4)2
=(-1)3+(![]() -4+4)2
-4+4)2
=-1+17
=16.
故(-a)3+(b+4)2的平方根是:±4.
-
科目: 来源: 题型:
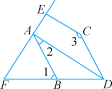
查看答案和解析>>【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)请你判断DA与CE的位置关系,并说明理由;
(2)若DA平分∠BDC,CE⊥AE于E,∠1=70°,试求∠FAB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
(1)若∠A=60°,∠ABD=24°,求∠ACF的度数;
(2)若EF=4,BF:FD=5:3,S△BCF=10,求点D到AB的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在四边形ABCD中,
 ,延长BC至点E,连接AE交CD于点F,使
,延长BC至点E,连接AE交CD于点F,使
 求证:
求证:  ;
; 求证:
求证:  ;
; 若BF平分
若BF平分 ,请写出
,请写出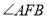 与
与 的数量关系______
的数量关系______ 不需证明
不需证明

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0)
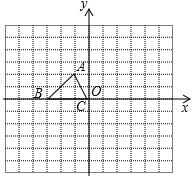
(1)请直接写出点A关于x轴对称的点
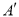 的坐标;
的坐标;(2)以C为位似中心,在x轴下方作△ABC的位似图形
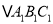 ,使放大前后位似比为1:2,请画出图形,并求出
,使放大前后位似比为1:2,请画出图形,并求出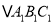 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,
 .已知关于x,y的二元一次方程
.已知关于x,y的二元一次方程 (m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
(m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
A.
 B.1 C.
B.1 C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

相关试题

