搜索
【题目】用平面去截一个几何体，若截面为长方形，则该几何体不可能是( )
A. 正方体 B. 长方体 C. 圆柱 D. 圆锥
参考答案：
【答案】D
【解析】
根据圆柱、圆锥、长方体、正方体的形状特点判断即可．
用平面截圆锥，得到的截面应该是椭圆，圆（截面与底面平行），三角形（截面经过顶点）唯独不可能是矩形，
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某文化用品商店计划同时购进一批A、B两种型号的计算器，若购进A型计算器10只和B型计算器8只，共需要资金880元;若购进A型计算器2只和B型计算器5只，共需要资金380只。
（1）求A、B两种型号的计算器每只进价各是多少元？
（2）该经销商计划购进这两种型号的计算器共50只，而可用于购买这两种型号的计算器的资金不超过2520元，根据市场行情，销售一只A型计算器可获利10元，销售一只B型计算器可获利15元，该经销商希望销售完这两种型号的计算器，所获利润不少于620元，则该经销商有哪几种进货方案？
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算题
（1）
（2）
（3）
（4）
（5）
（6）
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：﹣14+16÷（﹣2）3×|﹣3﹣1|．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a，b，c是△ABC的三条边长，化简|a+b﹣c|+|b﹣a﹣c|的结果为（ ）
A.2a+2bB.2a+2b﹣2cC.2b﹣2cD.2a
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，抛物线y=﹣
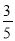[（x﹣2）2+n]与x轴交于点A（m﹣2，0）和B（2m+3，0）（点A在点B的左侧），与y轴交于点C，连结BC．（1）求m、n的值；
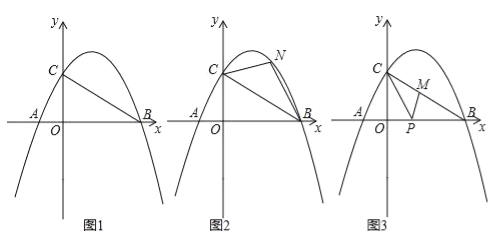
（2）如图2，点N为抛物线上的一动点，且位于直线BC上方，连接CN、BN．求△NBC面积的最大值；
（3）如图3，点M、P分别为线段BC和线段OB上的动点，连接PM、PC，是否存在这样的点P，使△PCM为等腰三角形，△PMB为直角三角形同时成立？若存在，求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD中，过A作AM⊥BC于M，交BD于E，过C作CN⊥AD于N，交BD于F，连结AF、CE．
（1）求证：△ABE≌△CDF；
（2）当四边形ABCD满足什么条件时，四边形AECF是菱形？证明你的结论．
相关试题
