【题目】如图,平行四边形ABCD中,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.

(1)求证:△ABE≌△CDF;
(2)当四边形ABCD满足什么条件时,四边形AECF是菱形?证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)四边形ABCD是菱形时,四边形AECF是菱形,证明见解析.
【解析】(1)根据ABCD为平行四边形,得到AD与BC平行且相等,由AM垂直于BC,CN垂直于AD,得到AM与CN平行,再由平行四边形ABCD,得到BC与AD平行,BC=AD,进而确定出AMCN为平行四边形,利用平行四边形的对边相等得到AN=CM,进而得到DN=BM,利用ASA得证;(2)利用菱形的性质可得AC⊥EF,由全等三角形的性质
可得AE=CF,由平行四边形的判定定理可得四边形AECF为平行四边形,利用菱形的判定定理得出结论.
证明:(1)∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,∴∠ABE=∠CDF,∠BAD=∠BCD,
∵MA⊥AN,NC⊥BC,∴∠BAM=∠DCN,
在△ABE和△CDF中,
∠ABE=∠CDF,AB=CD,∠BAM=∠DCN,
∴△ABE≌△CDF(SAS);
(2)四边形ABCD是菱形时,四边形AECF是菱形.
∵△ABE≌△CDF,∴AE=CF,
∵MA⊥AN,NC⊥BC,∴AM∥CN,∴四边形AECF为平行四边形,
∵四边形ABCD是菱形,∴AC⊥EF,∴四边形AECF为菱形.
“点睛”此题考查了平行四边形和菱形判定与性质,以及全等三角形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用平面去截一个几何体,若截面为长方形,则该几何体不可能是( )
A. 正方体 B. 长方体 C. 圆柱 D. 圆锥
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是△ABC的三条边长,化简|a+b﹣c|+|b﹣a﹣c|的结果为( )
A.2a+2bB.2a+2b﹣2cC.2b﹣2cD.2a
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=﹣
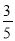 [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
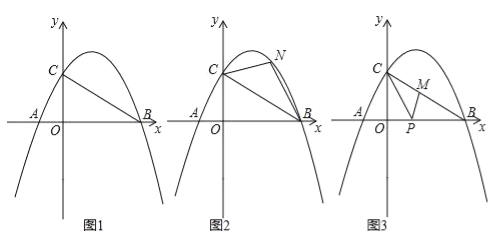
[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a是最小的自然数,b是最大的负整数,c是绝对值最小的有理数,则a-b+c的值为( )
A. -l B. 1 C. 0 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m<0,则m与它的5倍的相反数的差为 ( )
A. 4m B. -4m C. 6m D. -6m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,5个城市的国际标准时间(单位:时)表示在数轴上,那么北京时间某日20时应是( )

A. 伦敦时间11时 B. 巴黎时间13时
C. 纽约时间5时 D. 首尔时间19时
相关试题

