【题目】已知:抛物线![]() 经过点A(2,﹣3)和B(4,5).
经过点A(2,﹣3)和B(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G1,求图象G1的表达式;
(3)设B点关于对称轴的对称点为E,抛物线G2:![]() (a≠0)与线段EB恰有一个公共点,结合函数图象,求a的取值范围.
(a≠0)与线段EB恰有一个公共点,结合函数图象,求a的取值范围.

参考答案:
【答案】(1)![]() ,顶点坐标为(1,﹣4);(2)
,顶点坐标为(1,﹣4);(2)![]() ;(3)
;(3)![]() ≤a<
≤a<![]() .
.
【解析】
试题分析:(1)根据待定系数法求得即可;
(2)根据关于x轴对称的点的坐标特征即可求得;
(3)由于BE∥x轴,把B、E两点坐标代入![]() 可计算出对应的a的值,然后根据抛物线C2:
可计算出对应的a的值,然后根据抛物线C2:![]() (a≠0)与线段BE恰有一个公共点可确定a的范围.
(a≠0)与线段BE恰有一个公共点可确定a的范围.
试题解析:(1)把A(2,﹣3)和B(4,5)分别代入![]()
得:![]() ,解得:
,解得:![]() ,∴抛物线的表达式为:
,∴抛物线的表达式为:![]() .
.
∵![]() =
=![]() ,∴顶点坐标为(1,﹣4);
,∴顶点坐标为(1,﹣4);
(2)∵将抛物线沿x轴翻折,得到图象G1与原抛物线图形关于x轴对称,∴图象G1的表达式为:![]() ;
;
(3)∵B(4,5),对称轴:x=1,∴B点关于对称轴的对称点E点坐标为(﹣2,5),当G2过E点时,代入E(﹣2,5),则a=![]() ,当G2过B点时,代入B(4,5),则a=
,当G2过B点时,代入B(4,5),则a=![]() ,所以a的取值范围为
,所以a的取值范围为![]() ≤a<
≤a<![]() .
.
-
科目: 来源: 题型:
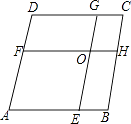
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )
A.6.5
B.6
C.5.5
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】方程2x=10的解是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
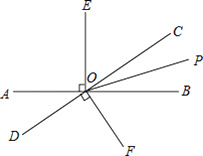
(1)图中除直角外,还有相等的角吗?请写出两对:①;② .
(2)如果∠COP=20°,则①∠BOP=°;②∠POF=°.
(3)∠EOC与∠BOF相等吗? , 理由是 .
(4)如果∠COP=20°,求∠DOE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l上有一点O,点A、B同时从O出发,在直线l上分别向左、向右作匀速运动,且A、B的速度比为1:2,设运动时间为ts.
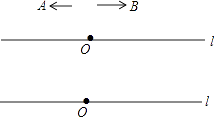
(1)当t=2s时,AB=12cm.此时,
①在直线l上画出A、B两点运动2秒时的位置,并回答点A运动的速度是cm/s; 点B运动的速度是cm/s.
②若点P为直线l上一点,且PA﹣PB=OP,求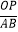 的值;
的值;
(2)在(1)的条件下,若A、B同时按原速向左运动,再经过几秒,OA=2OB. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读发现:如图①,在△ABC中,∠ACB=2∠B,∠ACB=90°,AD为∠BAC的平分线,且交BC于D,我们发现在AB上截取AE=AC,连结DE,可得AB=AC+CD(不需证明).
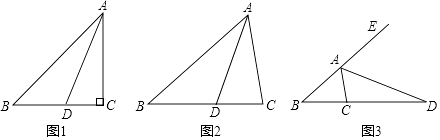
(1)探究:如图②,当∠ACB≠90°时,其他条件不变,线段AB、AC、CD又有怎样的数量关系,写出结果,并证明;
(2)拓展:如图③,当∠ACB=2∠B,∠ACB≠90°时,AD为△ABC的外角∠CAF的平分线,且交BC的延长线于点D,则线段AB、AC、CD又有怎样的数量关系?写出你的猜想,不需证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为
A.(2,-3)B.(-2,-3)C.(-2,3) D. (-3,-2)
相关试题

