【题目】如图,已知四边形ABCD中,∠B+∠D=180°,AC平分∠BAD,CE⊥AD,E为垂足.求证:AB+AD=2AE.

参考答案:
【答案】证明见解析.
【解析】
过点C作CH⊥AB,交AB的延长线于点H.利用角平分线性质得CH=CE,∠HCA=∠ECA,证△ACH≌△ACE(AAS),得AH=AE.∠HBC=∠D.再证△BHC≌△DEC(AAS),得HB=DE,
所以AB+AD=AB+AE+DE=AB+AE+HB=AH+AE=2AE.
证明:如图,过点C作CH⊥AB,交AB的延长线于点H.

∵AC平分∠BAD,CE⊥AD,
∴CH=CE,∠HCA=∠ECA(等角的余角相等).
在△ACH和△ACE中,
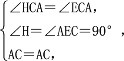
∴△ACH≌△ACE(AAS),
∴AH=AE.
又∵∠ABC+∠HBC=180°,
∠ABC+∠D=180°,
∴∠HBC=∠D.
在△BHC和△DEC中,
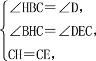
∴△BHC≌△DEC(AAS),
∴HB=DE,
∴AB+AD=AB+AE+DE=AB+AE+HB=AH+AE=2AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1 cm,△ACD的周长为12 cm,则△ABC的周长是( )

A. 13 cm B. 14 cm C. 15 cm D. 16 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C都是格点.
(1)将△ABC向左平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2;
(3)作出△ABC关于直线l对称的△A3B3C3,使A,B,C的对称点分别是A3,B3,C3;
(4)△A2B2C2与△A3B3C3成______________△A1B1C1与△A2B2C2成_____________(填“中心对称”或“轴对称”).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.

(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家批发商出售同样品牌的茶壶和茶杯,定价相同,茶壶每把30元,茶杯每只5元.两家都在进行优惠销售:甲店买一送一大酬宾(买一把茶壶赠送茶杯一只);乙店全场9折优惠(按实际价格的90%收费).某茶具店需茶壶5把,茶杯若干只(不少于5只).
(1)若设购买茶杯x只(x>5),则在甲店购买需付_____元,在乙店购买需付_____元;(用含x的代数式表示)
(2)当茶具店需购买10只茶杯时,到哪家商店购买较便宜?试加以说明;
(3)试求出当茶具店购买多少只茶杯时,在两家商店购买所需付的款一样多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是等边△ABC的外接圆,M是BC延长线上一点,连接AM交⊙O于点D,延长BD至点N,使得BN=AM,连接CN,MN.
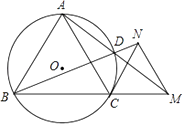
(1)判断△CMN的形状,并证明你的结论;
(2)求证:CN是⊙O的切线;
(3)若等边△ABC的边长是2,求ADAM的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A,点B的距离相等,点P对应的数是 .
(2)数轴上,点P到点A、点B的距离之和为5,则x的值为 ;
(3)当点P以每秒1个单位长度的速度从原点O向左运动,同时点B以每秒3个单位长度的速度沿数轴向左运动(点A保持不动),当点P到点A、点B的距离相等时,求运动时间t的值?
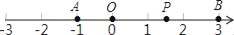
相关试题

