【题目】如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE. 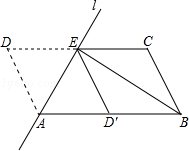
(1)求证:四边形BCED′是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2 .
参考答案:
【答案】
(1)证明:∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴AB ![]() DC,
DC,
∴CE ![]() D′B,
D′B,
∴四边形BCED′是平行四边形;
(2)∵BE平分∠ABC,
∴∠CBE=∠EBA,
∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∴AB2=AE2+BE2.

【解析】(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形;(2)利用平行线的性质结合勾股定理得出答案.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对平行四边形的判定与性质的理解,了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,高AD=12,则BC的长 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2﹣
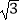 ,y=2+
,y=2+ 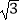 ,求下列代数式的值:
,求下列代数式的值:
(1)x2+2xy+y2;
(2)x2﹣y2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.

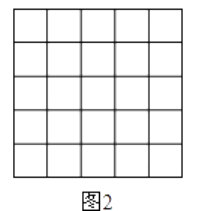
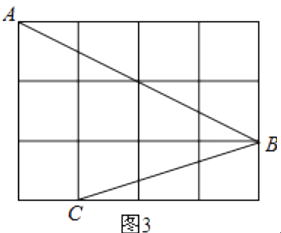
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、 、
、  ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
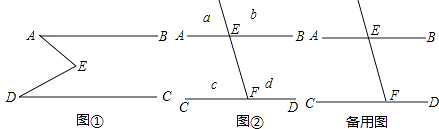
(1)探究猜想:
①若∠A=20°,∠D=40°,则∠AED=
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用:
如图②,射线FE与l1 , l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以点O为圆心,AB长为直径作圆,在⊙O上取一点C,延长AB至点D,连接DC,过点A作⊙O的切线交DC的延长线于点E,且∠DCB=∠DAC.
(1)求证:CD是⊙O的切线;
(2)若AD=6,tan∠DCB=
 ,求AE的长.
,求AE的长.
相关试题

