【题目】在△ABC中,AB=15,AC=13,高AD=12,则BC的长 .
参考答案:
【答案】14和4
【解析】解:(1)如图,锐角△ABC中,AC=13,AB=15,BC边上高AD=12, ∵在Rt△ACD中AC=13,AD=12,
∴CD2=AC2﹣AD2=132﹣122=25,
∴CD=5,
在Rt△ABD中AB=15,AD=12,由勾股定理得
BD2=AB2﹣AD2=152﹣122=81,
∴CD=9,
∴BC的长为BD+DC=9+5=14;(2)钝角△ABC中,AC=13,AB=15,BC边上高AD=12,
在Rt△ACD中AC=13,AD=12,由勾股定理得
CD2=AC2﹣AD2=132﹣122=25,
∴CD=5,
在Rt△ABD中AB=15,AD=12,由勾股定理得
BD2=AB2﹣AD2=152﹣122=81,
∴BD=9,
∴BC的长为DB﹣BC=9﹣5=4.
所以答案是14或4.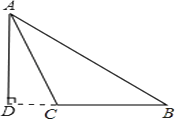
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )
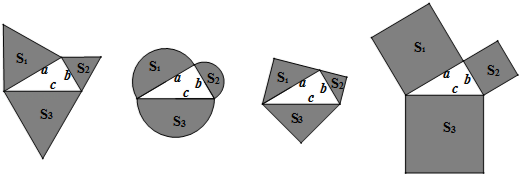
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a|=3,|b|=5,且a<b,求a+b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二元一次方程3a+b=9在正整数范围内的解的个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2﹣
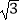 ,y=2+
,y=2+ 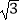 ,求下列代数式的值:
,求下列代数式的值:
(1)x2+2xy+y2;
(2)x2﹣y2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.
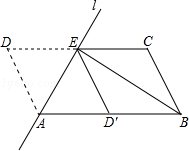
(1)求证:四边形BCED′是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2 .
相关试题

