【题目】(8分)已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.

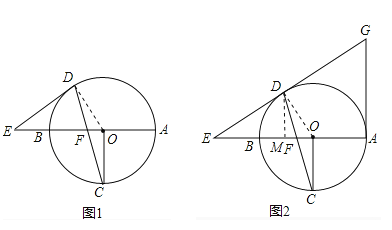
(1)如图①,求证:ED为⊙O的切线;
(2)如图②,直线ED与切线AG相交于G,且OF=2,⊙O的半径为6,求AG的长.
参考答案:
【答案】(1)见解析;(2)12
【解析】试题分析:(1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线;
(2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO的长度,结合∠DOE的正弦、余弦值可得出DM、MO的长度,根据切线的性质可知GA⊥EA,从而得出DM∥GA,根据相似三角形的判定定理即可得出△EDM∽△EGA,根据相似三角形的性质即可得出GA的长度
试题解析:解:(1)连接OD,∵ED=EF,∴∠EDF=∠EFD,∵∠EFD=∠CFO,∴∠EDF=∠CFO.∵OD=OC,∴∠ODF=∠OCF.∵OC⊥AB,∴∠CFO+∠OCF=∠EDF+∠ODF=∠EDO=90°,∴ED为⊙O的切线;
(2)连接OD,过点D作DM⊥BA于点M,由(1)可知△EDO为直角三角形,设ED=EF=a,EO=EF+FO=a+2,由勾股定理得,EO2=ED2+DO2,即(a+2)2=a2+62,解得,a=8,即ED=8,EO=10.∵sin∠EOD=![]() ,cos∠EOD=
,cos∠EOD=![]() ,∴DM=ODsin∠EOD=6×
,∴DM=ODsin∠EOD=6×![]() =
=![]() ,MO=ODcos∠EOD=6×
,MO=ODcos∠EOD=6×![]() =
=![]() ,∴EM=EO﹣MO=10﹣
,∴EM=EO﹣MO=10﹣![]() =
=![]() ,EA=EO+OA=10+6=16.
,EA=EO+OA=10+6=16.
∵GA切⊙O于点A,∴GA⊥EA,∴DM∥GA,∴△EDM∽△EGA,∴ ![]() ,即
,即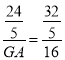 ,解得GA=12.
,解得GA=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
 ,
, ,点
,点 在
在 上,
上, .
.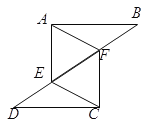
求证:(1)
 ;(2)
;(2) ∥
∥ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,
 ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.24)
≈2.24)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,

请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元)
2
种植树木利润y1(万元)
4
种植花卉利润y2(万元)
2
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示.在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,如果点P在线段BC上以3cm/s的速度由点B向点C运动,同时点Q在线段CA上由点C向点A运动.

(1)若点Q与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q与点P的运动速度不同,当点Q的运动速度是多少时能使△BPD与△CQP全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图点P是△ABC的边BC上的一动点,点E与点P关于直线AB成轴对称,连接EP交AB于点F,连接AP、EC相交于点O,连接AE.

(1)判断AE与AP的数量关系,并说明理由.
(2)在点P的运动过程中,当AE∥BC时,判断AP与BP的数量关系,并说明理由.
(3)若∠BAC=900,点P在运动过程中是否存在线段AP与线段EC互相平分的情况,若存在,请求出点P的位置;若不存在,请说明理由.
相关试题

