【题目】王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示. 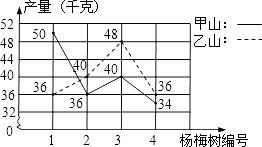
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
参考答案:
【答案】
(1)解: ![]() (千克),(1分)
(千克),(1分) ![]() (千克),
(千克),
总产量为40×100×98%×2=7840(千克)
(2)解: ![]() (千克2),
(千克2),
![]()
![]() (千克2),
(千克2),
∴S2甲>S2乙.
答:乙山上的杨梅产量较稳定
【解析】(1)根据平均数的求法求出平均数,再用样本估计总体的方法求出产量总和即可解答.(2)要比较哪个山上的杨梅产量较稳定,只要求出两组数据的方差,再比较即可解答.
【考点精析】通过灵活运用折线统计图和算术平均数,掌握能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比;总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的平分线,CA2是∠A1CD的平分线,BA3是∠A2BD的平分线,CA3是∠A2CD的平分线.若∠A1=α,则∠A2019=________.

-
科目: 来源: 题型:
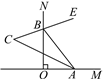
查看答案和解析>>【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠ABN,BE的反向延长线与∠BAO的平分线交于点C.
(1)当点A,B移动后,∠BAO=45°时,∠C=________;
(2)当点A,B移动后,∠BAO=60°时,∠C=________;
(3)由(1)(2)猜想∠C是否随点A,B的移动而发生变化,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=26°,∠C=70°,AD平分∠BAC,
AE⊥BC于点E,EF⊥AD于点F.
(1)求∠DAC的度数;
(2)求∠DEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF的两边相交于A、B和C、D,连接OA,此时有OA∥PE.
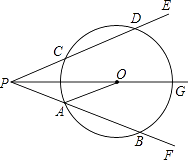
(1)求证:AP=AO;
(2)若tan∠OPB= ,求弦AB的长;
,求弦AB的长;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 , 能构成等腰梯形的四个点为或或 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某班师生组织植树活动,上午8时从学校出发,到植树地点植树后原路返校,如图为师生离校路程s与时间t之间的图象.请回答下列问题:
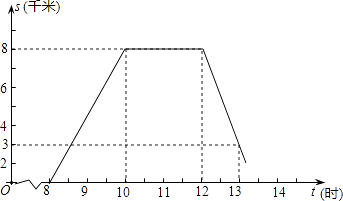
(1)求师生何时回到学校?
(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣
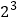 ﹣[(﹣3) ﹣2×
﹣[(﹣3) ﹣2× 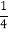 ﹣8.5]÷(﹣
﹣8.5]÷(﹣  )
) (2)
 ×
×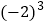 ﹣0.25×(﹣4)×(﹣3);
﹣0.25×(﹣4)×(﹣3);(3)(﹣1
 )﹣1
)﹣1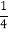 +(﹣
+(﹣  )﹣3
)﹣3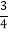 ﹣(﹣1
﹣(﹣1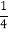 )
)(4)
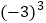 ÷4
÷4  ×(﹣
×(﹣ )+5﹣2×(﹣
)+5﹣2×(﹣  )
)
相关试题

