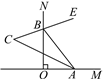
【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠ABN,BE的反向延长线与∠BAO的平分线交于点C.
(1)当点A,B移动后,∠BAO=45°时,∠C=________;
(2)当点A,B移动后,∠BAO=60°时,∠C=________;
(3)由(1)(2)猜想∠C是否随点A,B的移动而发生变化,并说明理由.
参考答案:
【答案】(1)(1)45°;(2)45°;(3)∠C不随点A,B的移动而发生变化,理由详见解析.
【解析】
(1)根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠ABN, 再根据角平分线的定义求出∠ABE和∠BAC, 然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)与(1)方法相同求解可得答案;
(3)与(1)的思路相同解答可得答案.
解:(1)根据三角形的外角性质,
∠ABN=∠AOB+∠BAO=90![]() +45
+45![]() =135
=135![]()
![]() BE平分∠ABN,AC平分∠BAO,
BE平分∠ABN,AC平分∠BAO,
![]() ∠ABE=
∠ABE=![]() ∠ABN=67.5
∠ABN=67.5![]() ,∠BAC=
,∠BAC=![]() ∠BAO=22.5
∠BAO=22.5![]() ,
,
![]() ∠C=∠ABE-∠BAC=45
∠C=∠ABE-∠BAC=45![]() ,
,
(2)同理:∠ABN=∠AOB+∠BAO=90![]() +60
+60![]() =150
=150![]()
![]() BE平分∠ABN,AC平分∠BAO,
BE平分∠ABN,AC平分∠BAO,
![]() ∠ABE=
∠ABE=![]() ∠ABN=75
∠ABN=75![]() ,∠BAC=
,∠BAC=![]() ∠BAO=30
∠BAO=30![]() ,
,
![]() ∠C=∠ABE-∠BAC=45
∠C=∠ABE-∠BAC=45![]() ,
,
(3)∠C不随点A,B的移动而发生变化.
理由:因为∠ABN是△ABO的外角,
所以∠ABN=∠AOB+∠BAO.
因为BE平分∠ABN,AC平分∠BAO,
所以∠ABE=![]() ∠ABN,∠BAC=
∠ABN,∠BAC=![]() ∠BAO,
∠BAO,
所以∠C=∠ABE-∠BAC=![]() (∠AOB+∠BAO)-
(∠AOB+∠BAO)-![]() ∠BAO=
∠BAO=![]() ∠AOB.
∠AOB.
因为∠AOB=∠MON=90°,
所以∠C=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活经验表明,靠墙摆放的梯子,当50°≤α≤70°时(α为梯子与地面所成的角),能够使人安全攀爬.现在有一长为6米的梯子AB,试求能够使人安全攀爬时,梯子的顶端能达到的最大高度AC.
(结果保留两个有效数字,sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的平分线,CA2是∠A1CD的平分线,BA3是∠A2BD的平分线,CA3是∠A2CD的平分线.若∠A1=α,则∠A2019=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=26°,∠C=70°,AD平分∠BAC,
AE⊥BC于点E,EF⊥AD于点F.
(1)求∠DAC的度数;
(2)求∠DEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
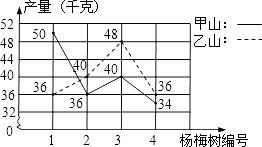
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF的两边相交于A、B和C、D,连接OA,此时有OA∥PE.
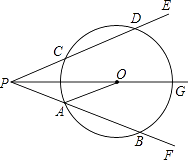
(1)求证:AP=AO;
(2)若tan∠OPB= ,求弦AB的长;
,求弦AB的长;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 , 能构成等腰梯形的四个点为或或 .
相关试题

