搜索
【题目】五张如图所示的长为
，宽为
的小长方形纸片，按如图的方式不重叠地放在矩形
中，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为
，当
的长度变化时，按照同样的放置方式，始终保持不变，则，
满足的关系式为（ ）
A.
B.
C.
D.
参考答案：
【答案】A
【解析】
表示出左上角与右下角部分的面积，求出之差，根据差与BC无关即可求出a与b的关系式
解：左上角阴影部分的长为AE，宽为AF=2b，右下角阴影部分的长为PC，宽为a，
∵AD=BC，即AE+ED=AE+a，BC=BP+PC=3b+PC，
∴AE+a=3b+PC，即AE-PC=3b-a，
∴阴影部分面积之差S=AEAF-PCCG=2b×AE-a×PC=2b（PC+3b-a）-aPC=（2b-a）PC+6b2-2ab，
则2b-a=0，即a=2b，
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点C在线段AB上，△DAC和△DBE都是等边三角形．
（1）求证：△DAB≌△DCE；
（2）求证：DA∥EC． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是将抛物线
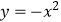平移后得到的抛物线，其对称轴为 
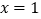，与x轴的一个交点为A 
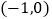，另一交点为B，与y轴交点为C．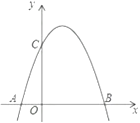
（1）求抛物线的函数表达式；
（2）若点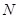
为抛物线上一点，且BC⊥NC，求点N的坐标；
（3）点P是抛物线上一点，点Q是一次函数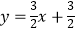
的图象上一点，若四边形OAPQ为平行四边形，这样的点P、Q是否存在？若存在，分别求出点P、Q的坐标，若不存在，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】生活常识：射到平面镜上的光线（入射光线）和变向后的光线（反射光线）与平面镜所夹的角相等．如图1，MN是平面镜，若入射光线AO与水平镜面夹角为∠1，反射光线OB与水平镜面夹角为∠2，则∠1=∠2．
（1）现象解释：如图2，有两块平面镜OM，ON，且OM⊥ON，入射光线AB经过两次反射，得到反射光线CD．已知：∠1=55°，求∠4的度数．
（2）尝试探究：如图3，有两块平面镜OM，ON，入射光线AB经过两次反射，得到反射光线CD，光线AB与CD相交于点E，若∠MON=46°，求∠CEB的度数．
（3）深入思考：如图4，有两块平面镜OM，ON，且∠MON=α，入射光线AB经过两次反射，得到反射光线CD，光线AB与CD所在的直线相交于点E，∠BED=β，α与β之间满足的等量关系是 ．（直接写出结果）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知顶点为（﹣3，﹣6）的抛物线y=ax2+bx+c经过点（﹣1，﹣4），则下列结论中错误的是（ ）
A.b2＞4ac
B.ax2+bx+c≥﹣6
C.若点（﹣2，m），（﹣5，n）在抛物线上，则m＞n
D.关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1 -
科目： 来源： 题型：
查看答案和解析>>【题目】某校课外兴趣小组在本校学生中开展“感动中国2014年度人物”先进事迹知晓情况专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为A、B、C、D四类．其中，A类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”，D类表示“不太了解”，划分类别后的数据整理如下表：
类别
A
B
C
D
频数
30
40
24
b
频率
a
0.4
0.24
0.06
（1）表中的a=________，b=________；
（2）根据表中数据，求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数；
（3）若该校有学生1000名，根据调查结果估计该校学生中类别为C的人数约为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在 Rt△ABC 中，∠C＝90°，AC＝8cm，BC＝6cm，M 在 AC上，且AM＝6cm，过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC，若动点 P 从点 A 出发，沿射线 AN 匀速运动，运动速度为 1cm/s，设点 P 运动时间为 t 秒．
(1)经过 秒时，Rt△AMP 是等腰直角三角形？
(2)经过几秒时，PM⊥MB？
(3)经过几秒时，PM⊥AB？
(4)当△BMP 是等腰三角形时，直接写出 t 的所有值．
相关试题
