【题目】探索与证明:
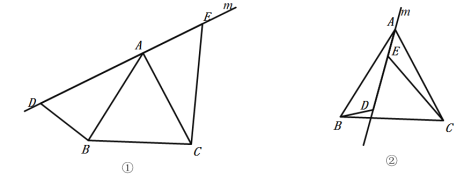
(1)如图①,直线![]() 经过正三角形
经过正三角形![]() 的顶点
的顶点![]() ,在直线
,在直线![]() 上取点
上取点![]() ,
,![]() ,使得
,使得![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明;
之间满足的数量关系,并予以证明;
(2)将(1)中的直线![]() 绕着点
绕着点![]() 逆时针方向旋转一个角度到如图②的位置,
逆时针方向旋转一个角度到如图②的位置,![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明.
之间满足的数量关系,并予以证明.
参考答案:
【答案】(1)DE=BD+CE,证明见解析;(2)CE =BD+DE,证明见解析
【解析】
(1)根据等边三角形的性质可得AB=CA,∠BAC=60°,然后根据已知条件可得![]() ,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据DE=AE+AD和等量代换即可得出结论;
,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据DE=AE+AD和等量代换即可得出结论;
(2)根据等边三角形的性质可得AB=CA,∠BAC=60°,然后根据已知条件可得![]() ,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据AD= AE+DE和等量代换即可得出结论;
,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据AD= AE+DE和等量代换即可得出结论;
解:(1)DE=BD+CE,证明如下
∵△ABC为等边三角形
∴AB=CA,∠BAC=60°
∵![]() ,
,![]()
∴![]()
∴∠ABD+∠BAD=180°-∠ADB=120°
∠CAE+∠BAD=180°-∠BAC=120°
∴∠ABD=∠CAE
在△ABD和△CAE中
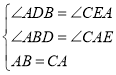
∴△ABD≌△CAE
∴BD=AE,AD= CE
∴DE=AE+AD= BD+CE;
(2)CE =BD+DE,证明如下
∵△ABC为等边三角形
∴AB=CA,∠BAC=60°
∵![]() ,
,![]()
∴![]()
∴∠ABD+∠BAD=180°-∠ADB=60°
∠CAE+∠BAD=∠BAC=60°
∴∠ABD=∠CAE
在△ABD和△CAE中
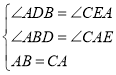
∴△ABD≌△CAE
∴BD=AE,AD= CE
∵AD= AE+DE
∴CE= BD+DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强环保意识,某社区计划开展一次“减碳环保,减少用车时间”的宣传活动,对部分家庭五月份的平均每天用车时间进行了一次抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)本次抽样调查了多少个家庭?
(2)将图①中的条形图补充完整,直接写出用车时间的中位数落在哪个时间段内;
(3)求用车时间在1~1.5小时的部分对应的扇形圆心角的度数;
(4)若该社区有车家庭有1600个,请你估计该社区用车时间不超过1.5小时的约有多少个家庭?
-
科目: 来源: 题型:
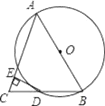
查看答案和解析>>【题目】如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b的图象与反比例函数y=
 的图象交于点A(2,1),B(-1,n)两点.
的图象交于点A(2,1),B(-1,n)两点.(1)求反比例函数的解析式;
(2)求一次例函数的解析式;
(3)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为160元,200元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段
销售数量
销售收入/元
A种型号/台
B种型号/台
第1周
3
5
1800
第2周
4
10
3200
(1)A、B两种型号的电风扇的销售单价是多少?
(2)若该超市准备用不多于5400元的金额再次采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
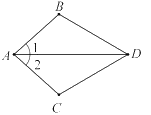
A. ∠ADB=∠ADCB. ∠B=∠CC. DB=DCD. AB=AC
相关试题

