【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)△AOD为直角三角形.
【解析】试题分析:
试题解析:(1)利用有一个角是60°的等腰三角形是等边三角形易证.
(2) 将△BOC绕点C按顺时针方向旋转60°得△ADC,利用(1)可得△AOD是直角三角形.
试题解析:(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠OCD=60°,CO=CD,
∴△OCD是等边三角形;
(2)解:△AOD为直角三角形.
理由:∵△COD是等边三角形.
∴∠ODC=60°,
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠ADC=∠BOC=α,
∴∠ADC=∠BOC=150°,
∴∠ADO=∠ADC﹣∠CDO=150°﹣60°=90°,于是△AOD是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若10m=5,10n=3,则102m+3n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左到右的变形错误的是( )
A. (y﹣x)2=(x﹣y)2 B. ﹣a﹣b=﹣(a+b)
C. (a﹣b)3=﹣(b﹣a)3 D. ﹣m+n=﹣(m+n)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,回答问题:
解方程x4﹣5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2﹣5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=﹣1,x3=2,x4=﹣2.
(1)在由原方程得到方程①的过程中,利用换元法达到 的目的,体现了数学的转化思想.
(2)解方程
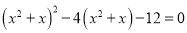 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为元时,该服装店平均每天的销售利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若是x2+(m-1)x+9是完全平方式,则m的值是( )
A. 7B. -5C. ±6D. 7或-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】1纳米=0.000000001米,则0.5纳米用科学记数法表示为( )
A. 0.5×10-9米B. 5×10-8 米C. 5×10-9米D. 5×10-10米
相关试题

