【题目】如图,已知Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形的对角线交于点O,连结OC.已知AC=5,OC=6 ![]() ,则另一直角边BC的长为 .
,则另一直角边BC的长为 . 
参考答案:
【答案】4
【解析】过O作OF垂直于BC,再过A作AM垂直于OF,由四边形ABDE为正方形,得到OA=OB,∠AOB为直角,可得出两个角互余,再由AM垂直于MO,得到△AOM为直角三角形,其两个锐角互余,利用同角的余角相等可得出一对角相等,再由一对直角相等,OA=OB,利用AAS可得出△AOM与△BOF全等,由全等三角形的对应边相等可得出AM=OF,OM=FB,由三个角为直角的四边形为矩形得到ACFM为矩形,根据矩形的对边相等可得出AC=MF,AM=CF,等量代换可得出CF=OF,即△COF为等腰直角三角形,由斜边OC的长,利用勾股定理求出OF与CF的长,根据OF﹣MF求出OM的长,即为FB的长,由CF+FB即可求出BC的长.解法一:如图1所示,过O作OF⊥BC,过A作AM⊥OF,∵四边形ABDE为正方形,∴∠AOB=90°,OA=OB,∴∠AOM+∠BOF=90°,又∠AMO=90°,∴∠AOM+∠OAM=90°,∴∠BOF=∠OAM,在△AOM和△BOF中, 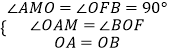 ,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6
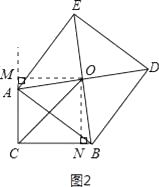
,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6 ![]() ,∴根据勾股定理得:CF2+OF2=OC2 , 解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6
,∴根据勾股定理得:CF2+OF2=OC2 , 解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6 ![]() ,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.
,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.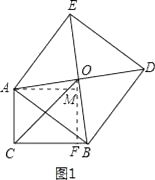
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)a-6ab+9ab2;(2)x2(x-y)+y2(y-x).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个5倍的放大镜去观察一个三角形,对此,四位同学有如下说法:
甲说:三角形的每个内角都扩大到原来的5倍;
乙说:三角形的每条边都扩大到原来的5倍;
丙说:三角形的面积扩大到原来的5倍;
丁说:三角形的周长都扩大到原来的5倍.上述说法中正确的是( )
A. 甲和乙B. 乙和丙C. 丙和丁D. 乙和丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程2x﹣m﹣5=0的解是x=﹣2,则m的值为( )
A.9
B.﹣9
C.1
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF; ②△EFG≌△GBE; ③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.
其中正确的是.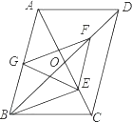
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一矩形长20 cm,宽10 cm,另一与它相似的矩形的一边长为10 cm,求另一边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”,等积线被这个平面图形截得的线段叫做该图形的“等积线段”(例如三角形的中线就是三角形的等积线段).已知菱形的边长为4,且有一个内角为60°,设它的等积线段长为m,则m的取值范围是.
相关试题

