【题目】平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF; ②△EFG≌△GBE; ③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.
其中正确的是.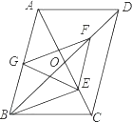
参考答案:
【答案】①②④
【解析】试题解析:令GF和AC的交点为点P,如图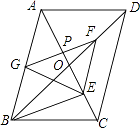
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF= ![]() CD,
CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴∠FEG=∠BGE(两直线平行,内错角相等),
∵点G为AB的中点,
∴BG= ![]() AB=
AB= ![]() CD=FE,
CD=FE,
在△EFG和△GBE中,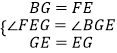 ,
,
∴△EFG≌△GBE(SAS),即②成立,
∴∠EGF=∠GEB,
∴GF∥BE(内错角相等,两直线平行),
∵BD=2BC,点O为平行四边形对角线交点,
∴BO= ![]() BD=BC,
BD=BC,
∵E为OC中点,
∴BE⊥OC,
∴GP⊥AC,
∴∠APG=∠EPG=90°
∵GP∥BE,G为AB中点,
∴P为AE中点,即AP=PE,且GP= ![]() BE,
BE,
在△APG和△EGP中,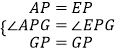 ,
,
∴△APG≌△EPG(SAS),
∴AG=EG= ![]() AB,
AB,
∴EG=EF,即①成立,
∵EF∥BG,GF∥BE,
∴四边形BGFE为平行四边形,
∴GF=BE,
∵GP= ![]() BE=
BE= ![]() GF,
GF,
∴GP=FP,
∵GF⊥AC,
∴∠GPE=∠FPE=90°
在△GPE和△FPE中,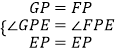 ,
,
∴△GPE≌△FPE(SAS),
∴∠GEP=∠FEP,
∴EA平分∠GEF,即④成立.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个5倍的放大镜去观察一个三角形,对此,四位同学有如下说法:
甲说:三角形的每个内角都扩大到原来的5倍;
乙说:三角形的每条边都扩大到原来的5倍;
丙说:三角形的面积扩大到原来的5倍;
丁说:三角形的周长都扩大到原来的5倍.上述说法中正确的是( )
A. 甲和乙B. 乙和丙C. 丙和丁D. 乙和丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程2x﹣m﹣5=0的解是x=﹣2,则m的值为( )
A.9
B.﹣9
C.1
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形的对角线交于点O,连结OC.已知AC=5,OC=6
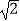 ,则另一直角边BC的长为 .
,则另一直角边BC的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一矩形长20 cm,宽10 cm,另一与它相似的矩形的一边长为10 cm,求另一边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”,等积线被这个平面图形截得的线段叫做该图形的“等积线段”(例如三角形的中线就是三角形的等积线段).已知菱形的边长为4,且有一个内角为60°,设它的等积线段长为m,则m的取值范围是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有A、B两个餐厅,甲、乙两名学生各自随机选择其中一个餐厅用餐,请用列表或画树状图的方法解答:
(1)甲、乙两名学生在同一餐厅用餐的概率;
(2)甲、乙两名学生至少有一人在B餐厅的概率.
相关试题

