【题目】某工地有72m2的墙面需要粉刷.若安排4名一级技工粉刷一天,结果还剩12m2墙面未能刷完;同样时间内安排6名二级技工去粉刷,则刚好全部刷完.己知每名一级技工比二级技工一天多粉刷3m2墙面.设每一名一级技工一天粉刷墙面xm2.
(1)每名二级技工一天粉刷墙面_____m2(用含x的式子表示);
(2)求每名一级技工、二级技工一天分别能粉刷多少m2墙面?
(3)每名一级技工一天的施工费是300元,每名二级技工一天的施工费是200元.若另一工地有540m2的墙面需要粉刷,要求一天完工且施工总费用不超过10600元,则至少需要_____名二级技工(直接写出结果).
参考答案:
【答案】(1)(x-3);(2)15m2、12m2;(3)5.
【解析】
(1)根据每一名一级技工一天粉刷墙面xm2,每名一级技工比二级技工一天多粉刷3m2墙面,即可写出每名二级技工一天粉刷墙面为(x-3)m2;(2)根据题意可列出方程![]() =
=![]() ,即可求解;(3)设至少需要y名二级技工,则需要
,即可求解;(3)设至少需要y名二级技工,则需要![]() 名一级技工,根据题意可列出不等式,即可进行求解.
名一级技工,根据题意可列出不等式,即可进行求解.
(1) 根据每一名一级技工一天粉刷墙面xm2,每名一级技工比二级技工一天多粉刷3m2墙面,即可写出每名二级技工一天粉刷墙面为(x-3)m2;
(2)依题意列方程:![]() =
=![]() ;
;
解得x=15,经检验x=15是原方程的解,
即每名一级技工和二级技工一天分别能粉刷15m2、12m2墙面;
(3) 设至少需要y名二级技工,则需要![]() 名一级技工,
名一级技工,
依题意得![]()
解得y≥5,
故至少需要5名二级技工.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF.
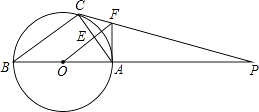
(1)判断AF与⊙O的位置关系并说明理由;
(2)已知半径为20,AF=15,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,A(-2,1),B(-3,4),C(-1,3),过点(l,0)作x轴的垂线
 .
.(1)作出△ABC关于直线
 的轴对称图形△
的轴对称图形△ ;
;(2)直接写出A1(___,___),B1(___,___),C1(___,___);
(3)在△ABC内有一点P(m,n),则点P关于直线
 的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).
的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是AB上一点,DF交AC于点E,AE=EC,DE=EF,则下列说法中:①∠ADE=∠EFC;②∠ADE+∠ECF+∠FEC=180°;③∠B+∠BCF=180°;④S△ABC=S四边形DBCF.正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
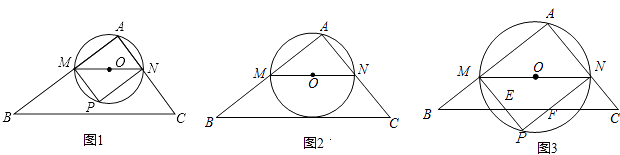
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切;
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.若a<0,则当x≤1时,y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=60°,D为AB上一点,连接CD.
(1)如图1,若∠BCA=90°,CD⊥AB,则
 =______(直接写出结果).
=______(直接写出结果).(2)如图2,若BD=AC,E为CD的中点,AE与BC存在怎样的数量关系,判断并说明理由;
(3)如图3,CD平分∠ACB,BF平分∠ABC,交CD于F.若BF=AC,求∠ACD的度数.

相关试题

