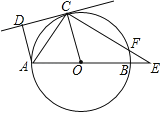
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上的一点,CE交⊙O于点F,连接OC,AC,若∠DAO=105°,∠E=30°.
(Ⅰ)求∠OCE的度数;
(Ⅱ)若⊙O的半径为2![]() ,求线段EF的长.
,求线段EF的长.
参考答案:
【答案】(Ⅰ)45°;(Ⅱ)2![]() ﹣2.
﹣2.
【解析】分析:
(1)由CD是⊙O的切线可得OC⊥CD,结合AD⊥CD于点D可得OC∥AD,从而可得∠COE=∠DAE=105°,结合∠E=30°即可得到∠OCE=45°;
(2)如下图,过点O作OM⊥CF于点M,则CM=MF结合∠OCE=45°,OC=![]() 即可得到OM=CM=2=MF,结合∠E=30°可得OE=2OM=4,则由勾股定理可得ME=
即可得到OM=CM=2=MF,结合∠E=30°可得OE=2OM=4,则由勾股定理可得ME=![]() ,从而可得EF=ME-MF=
,从而可得EF=ME-MF=![]() .
.
详解:
(Ⅰ)∵CD是⊙O的切线,
∴OC⊥CD,又AD⊥CD,
∴AD∥OC,
∴∠COE=∠DAO=105°,
又∵∠E=30°,
∴∠OCE=180°﹣∠COE﹣∠E=45°;
(Ⅱ)如下图,过点O作OM⊥CE于M,
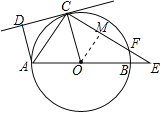
∴ CM=MF,∠OMC=∠OME=90°,
∵∠OCE=45°,
∴OM=CM=2=MF,
∵∠E=30°,
∴在Rt△OME中,OE=2OM=4,
∴ME=![]() ,
,
∴EF=ME-MF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
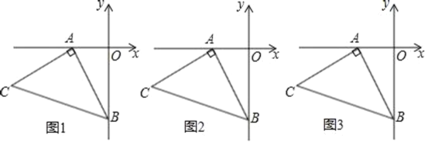
(1)求C点的坐标;
(2)如图1,在平面内是否存在一点H,使得以A、C、B、H为顶点的四边形为平行四边形?若存在,请直接写出H点坐标;若不存在,请说明理由;
(3)如图1点M(1,﹣1)是第四象限内的一点,在y轴上是否存在一点F,使得|FM﹣FC|的值最大?若存在,请求出F点坐标;若不存在,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:

(1)按第①行数排列的规律,第7个数是____,第
 个数是_______(用含
个数是_______(用含 的式子表示)
的式子表示)(2)观察第②行数与第①行数的关系,第②行第
 个数是________(用含
个数是________(用含 的式子表示)
的式子表示)观察第③行数与第①行数的关系,第③行第
 个数是__________(用含
个数是__________(用含 的式子表示)
的式子表示)(3)取每行数的第8个数,计算这三个数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简题.
(1)合并下列同类项: 4a2-3b2+2ab-4a2-3b2+5ba
(2)先化简,再求值:2(3x2﹣4xy)﹣4(2x2﹣3xy﹣1),其中|x﹣1|+(y+2)2=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:b是最小的正整数,且a、b满足(c﹣6)2+|a+b|=0,请回答问题
(1)请直接写出a、b、c的值.a= ,b= ,c=
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在A、B之间运动时,请化简式子:|x+1|﹣|x﹣1|﹣2|x+5|(请写出化简过程)
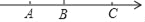
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒n(n>0)个单位长度的速度向左运动,同时,点B和点C分别以每秒2n个单位长度和5n个单位长度的速度向右运动,假设经过t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机动车出发前油箱内有42升油,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图,回答下列问题(1)机动车行驶________小时后加油,中途加油_______升;(2)求加油前油箱剩余油量Q与行驶时间t的函数关系,并直接写出自变量t的取值范围;(3)如果加油站距目的地还有230千米,车速为40千米/时,要到达目的地,油箱中的油是否够用?请说明理由。
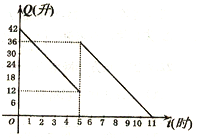
-
科目: 来源: 题型:
查看答案和解析>>【题目】滴滴打车为市民的出行带来了很大的方便,小亮调查了若干市民一周内使用滴滴打车的时间t(单位:分),将获得的数据分成四组,绘制了如下统计图,请根据图中信息,解答下列问题:
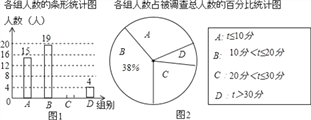
(1)这次被调查的总人数是多少?
(2)试求表示C组的扇形圆心角的度数,并补全条形统计图;
(3)若全市的总人数为666万,试求全市一周内使用滴滴打车超过20分钟的人数大约有多少?
相关试题

