【题目】已知曲线C上任意一点M到点F(0,1)的距离比它到直线l:y=﹣2的距离小1. (Ⅰ)求曲线C的方程;
(Ⅱ)斜率不为0且过点P(2,2)的直线m与曲线C交于A,B两点,设 ![]() =λ
=λ ![]() ,当△AOB的面积为4
,当△AOB的面积为4 ![]() 时(O为坐标原点),求λ的值.
时(O为坐标原点),求λ的值.
参考答案:
【答案】解:(Ⅰ)∵点M到点F(0,1)的距离比它到直线l:y=﹣2的距离小于1, ∴点M在直线l的上方,点M到F(1,0)的距离与它到直线l′:y=﹣1的距离相等,
∴点M的轨迹C是以F为焦点,l′为准线的抛物线,
所以曲线C的方程为x2=4y.
(Ⅱ)当直线m的斜率不存在时,它与曲线C只有一个交点,不合题意,
设直线m的方程为y﹣2=k(x﹣2),即y=kx+(2﹣2k),
代入x2=4y,得x2﹣4kx+8(k﹣1)=0,(*)
△=16(k2﹣2k+2)>0对k∈R恒成立,
所以,直线m与曲线C恒有两个不同的交点,
设交点A,B的坐标分别为A(x1 , y1),B(x2 , y2),
则x1+x2=4k,x1x2=8(k﹣1),
∴|AB|= ![]() ,
,
又O到直线AB的距离d= ![]() ,
,
∴S△AOB= ![]() |AB|d=4|k﹣1|
|AB|d=4|k﹣1| ![]() =4
=4 ![]() =4
=4 ![]() ,
,
∴(k﹣1)2(k2﹣2k+2)=(k﹣1)4+(k﹣1)2=2,解得(k﹣1)2=1,∴k=0(舍)或k=2.
把k=2代入方程(*),得x2﹣8x+8=0,解得x=4±2 ![]() ,
,
∵ ![]() =λ
=λ ![]() ,∴λ=
,∴λ=  =3﹣2
=3﹣2 ![]() 或λ=
或λ=  =3+2
=3+2 ![]()
【解析】(Ⅰ)由题设知:点M的轨迹C是以F为焦点,以直线y=﹣1为准线的抛物线,由此能求出曲线C的方程.(Ⅱ)设直线m的方程为y=kx+(2﹣2k),代入抛物线方程,由韦达定理、弦长公式、点到直线的距离公式得出三角形的面积,求出k,得出A,B的横坐标,根据相似比得出λ的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2asin2x﹣2
 asinxcosx+1在区间[0,
asinxcosx+1在区间[0,  ]的最大值为4,求实数a的值.
]的最大值为4,求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知斜三棱柱ABC﹣A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
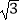 ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C. 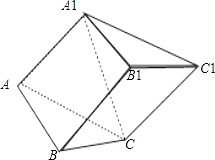
(1)求侧棱A1A与底面ABC所成角的大小;
(2)求侧面A1ABB1与底面ABC所成二面角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题获得学分2分,便可通过考察.已知6道备选题中考生甲有4题能正确完成:考生乙每题正确完成的概率都是
 ,且每题正确完成与否互不影响.求: (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
,且每题正确完成与否互不影响.求: (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(Ⅱ)请你判断两考生的实验操作学科能力,比较他们能通过本次考查的可能性大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ln2(x﹣1)﹣
 ﹣x+3. (Ⅰ)求函数f(x)的单调区间;
﹣x+3. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若当x≥1时,不等式(x+1)x+m≤exx+m恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)如果关于x的不等式|x+3|+|x﹣2|<a的解集不是空集,求参数a的取值范围; (Ⅱ)已知正实数a,b,且h=min{a,
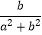 },求证:0<h≤
},求证:0<h≤  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若对任意的实数a,函数f(x)=(x﹣1)lnx﹣ax+a+b有两个不同的零点,则实数b的取值范围是( )
A.(﹣∞,﹣1]
B.(﹣∞,0)
C.(0,1)
D.(0,+∞)
相关试题

