【题目】已知函数f(x)=ln2(x﹣1)﹣ ![]() ﹣x+3. (Ⅰ)求函数f(x)的单调区间;
﹣x+3. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若当x≥1时,不等式(x+1)x+m≤exx+m恒成立,求实数m的取值范围.
参考答案:
【答案】解:(Ⅰ)由f(x)=ln2(x﹣1)﹣ ![]() ﹣x+3, 得f′(x)=
﹣x+3, 得f′(x)= ![]() ln(x﹣1)+
ln(x﹣1)+ ![]() ﹣1=
﹣1= ![]()
= ![]() (x﹣1>0),
(x﹣1>0),
令g(x)=2(x﹣1)ln(x﹣1)﹣x2+2x,
g′(x)=2ln(x﹣1)+2﹣2x+2=2ln(x﹣1)﹣2x+4,
再令t(x)=2ln(x﹣1)﹣2x+4,
t′(x)= ![]() ,当x∈(1,2)时,t′(x)>0,t(x)为增函数,
,当x∈(1,2)时,t′(x)>0,t(x)为增函数,
当x∈(2,+∞)时,t′(x)<0,t(x)为减函数,
∴t(x)max=t(2)=0,
∴g′(x)≤0,则g(x)在(1,+∞)上为减函数,
又当x→1+时,g(x)→﹣∞,
∴f′(x)<0,
则f(x)在(1,+∞)上为单调减函数;
(Ⅱ)由(x+1)x+m≤exx+m恒成立,即(x+m)ln(x+1)≤1+(x+m)lnx恒成立,
∴(x+m)ln ![]() ≤1,也即x+m
≤1,也即x+m ![]() ,
,
∴m ![]() 对x≥1恒成立.
对x≥1恒成立.
令h(x)= ![]() ,
,
则h′(x)=  <0(x≥1),
<0(x≥1),
∴h(x)在[1,+∞)上为减函数,则h(x)≤h(1)=﹣ln2﹣1,
又当x→+∞时,h(x)→﹣∞,
∴h(x)在[1,+∞)上无最小值,
则满足m ![]() 对x≥1恒成立的m不存在.
对x≥1恒成立的m不存在.
【解析】(Ⅰ)求出原函数的导函数,可得f′(x)= ![]() (x﹣1>0),令g(x)=2(x﹣1)ln(x﹣1)﹣x2+2x,求导可得g′(x)=2ln(x﹣1)+2﹣2x+2=2ln(x﹣1)﹣2x+4,再令t(x)=2ln(x﹣1)﹣2x+4,利用导数求得t(x)max=t(2)=0,得g′(x)≤0,则g(x)在(1,+∞)上为减函数,进一步说明f′(x)<0,得到f(x)在(1,+∞)上为单调减函数;(Ⅱ)由(x+1)x+m≤exx+m恒成立,即(x+m)ln(x+1)≤1+(x+m)lnx恒成立,分离参数m,可得m
(x﹣1>0),令g(x)=2(x﹣1)ln(x﹣1)﹣x2+2x,求导可得g′(x)=2ln(x﹣1)+2﹣2x+2=2ln(x﹣1)﹣2x+4,再令t(x)=2ln(x﹣1)﹣2x+4,利用导数求得t(x)max=t(2)=0,得g′(x)≤0,则g(x)在(1,+∞)上为减函数,进一步说明f′(x)<0,得到f(x)在(1,+∞)上为单调减函数;(Ⅱ)由(x+1)x+m≤exx+m恒成立,即(x+m)ln(x+1)≤1+(x+m)lnx恒成立,分离参数m,可得m ![]() 对x≥1恒成立.令h(x)=
对x≥1恒成立.令h(x)= ![]() ,由导数求其值域,可知h(x)在[1,+∞)上无最小值,则满足m
,由导数求其值域,可知h(x)在[1,+∞)上无最小值,则满足m ![]() 对x≥1恒成立的m不存在.
对x≥1恒成立的m不存在.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]()
![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知斜三棱柱ABC﹣A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
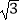 ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C. 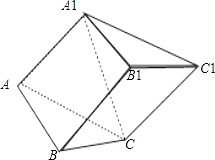
(1)求侧棱A1A与底面ABC所成角的大小;
(2)求侧面A1ABB1与底面ABC所成二面角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题获得学分2分,便可通过考察.已知6道备选题中考生甲有4题能正确完成:考生乙每题正确完成的概率都是
 ,且每题正确完成与否互不影响.求: (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
,且每题正确完成与否互不影响.求: (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(Ⅱ)请你判断两考生的实验操作学科能力,比较他们能通过本次考查的可能性大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C上任意一点M到点F(0,1)的距离比它到直线l:y=﹣2的距离小1. (Ⅰ)求曲线C的方程;
(Ⅱ)斜率不为0且过点P(2,2)的直线m与曲线C交于A,B两点,设 =λ
=λ  ,当△AOB的面积为4
,当△AOB的面积为4  时(O为坐标原点),求λ的值.
时(O为坐标原点),求λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)如果关于x的不等式|x+3|+|x﹣2|<a的解集不是空集,求参数a的取值范围; (Ⅱ)已知正实数a,b,且h=min{a,
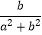 },求证:0<h≤
},求证:0<h≤  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若对任意的实数a,函数f(x)=(x﹣1)lnx﹣ax+a+b有两个不同的零点,则实数b的取值范围是( )
A.(﹣∞,﹣1]
B.(﹣∞,0)
C.(0,1)
D.(0,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为 .

相关试题

