【题目】如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为(4,0),点B的坐标为(0,1),点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE.
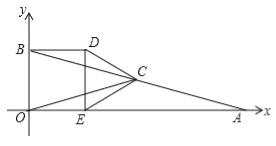
(1)线段OC的长为 ;
(2)求证:△CBD≌△COE;
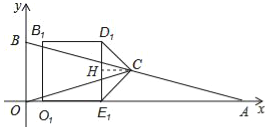
(3)将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1,其中点O,B,D,E的对应点分别为点O1,B1,D1,E1,连接CD,CE,设点E的坐标为(a,0),其中a≠2,△CD1E1的面积为S.
①当1<a<2时,请直接写出S与a之间的函数表达式;
②在平移过程中,当S=![]() 时,请直接写出a的值.
时,请直接写出a的值.
参考答案:
【答案】(1)![]() ;(2)详见解析;(3)①S=﹣
;(2)详见解析;(3)①S=﹣![]() a+1;②当S=
a+1;②当S=![]() 时,a=
时,a=![]() 或
或![]() .
.
【解析】
试题分析:(1)由点A的坐标为(4,0),点B的坐标为(0,1),根据勾股定理求得AB的长,再由点C为边AB的中点,根据直角三角形斜边的中线等于斜边的一半,即可求得线段OC的长;(2)由四边形OBDE是正方形,直角三角形斜边的中线等于斜边的一半,易得BD=OE,BC=OC,∠CBD=∠COE,即可证得:△CBD≌△COE;(3)①首先根据题意画出图形,然后过点C作CH⊥D1E1于点H,可求得△CD1E1的高与底,继而求得答案;
②分别从1<a<2与a>2去分析求解即可求得答案.
试题解析:(1)∵点A的坐标为(4,0),点B的坐标为(0,1),
∴OA=4,OB=1,
∵∠AOB=90°,
∴AB=![]() ,
,
∵点C为边AB的中点,
∴OC=![]() AB=
AB=![]() ;
;
(2)证明:∵∠AOB=90°,点C是AB的中点,
∴OC=BC=![]() AB,
AB,
∴∠CBO=∠COB,
∵四边形OBDE是正方形,
∴BD=OE,∠DBO=∠EOB=90°,
∴∠CBD=∠COE,
在△CBD和△COE中,
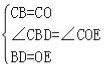 ,
,
∴△CBD≌△COE(SAS);
(3)①解:过点C作CH⊥D1E1于点H,
∵C是AB边的中点,
∴点C的坐标为:(2,![]() )
)
∵点E的坐标为(a,0),1<a<2,
∴CH=2﹣a,
∴S=![]() D1E1CH=
D1E1CH=![]() ×1×(2﹣a)=﹣
×1×(2﹣a)=﹣![]() a+1;
a+1;
②当1<a<2时,S=﹣![]() a+1=
a+1=![]() ,
,
解得:a=![]() ;
;
当a>2时,同理:CH=a﹣2,
∴S=![]() D1E1CH=
D1E1CH=![]() ×1
×1![]() a﹣1,
a﹣1,
∴S=![]() a﹣1=
a﹣1=![]() ,
,
解得:a=![]() ,
,
综上可得:当S=![]() 时,a=
时,a=![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当k=__________时,多项式x-1与2-kx的乘积中不含x的一次项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意的非零实数m,关于x的方程x2-4x-m2=0的根的情况是( )
A. 有两个正实数根 B. 有两个负实数根
C. 有一个正实数根,一个负实数根 D. 没有实数根
-
科目: 来源: 题型:
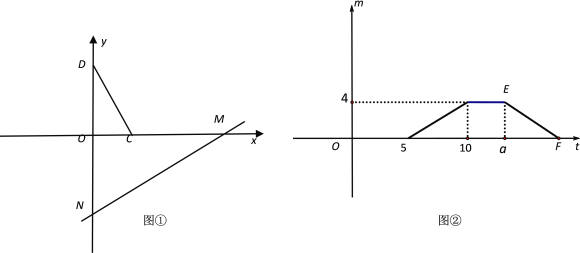
查看答案和解析>>【题目】如图①,将□ABCD置于直角坐标系中,其中BC边在x轴上(B在C的左侧),点D坐标为(0,4),直线MN:y=
 x-6沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t(s),m与t的函数图像如图②所示.
x-6沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t(s),m与t的函数图像如图②所示.(1)填空:点C的坐标为 ;在平移过程中,该直线先经过B、D中的哪一点? ;(填“B”或“D”)
(2)点B的坐标为 ,a= .
(3)求图②中线段EF的函数关系式;
(4)t为何值时,该直线平分□ABCD的面积?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是⊙O的内接三角形,且∠BOC=80°则∠BAC=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
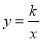 的图象与一次函数
的图象与一次函数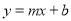 的图象交于
的图象交于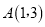 ,
, 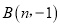 两点.
两点.(1)求反比例函数与一次函数的解析式;
(2)求
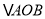 的面积.
的面积.(3)根据图象回答:当
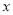 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.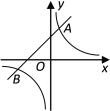
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正多边形的每个内角都是150°,那么这个多边形的内角和为______.
相关试题

