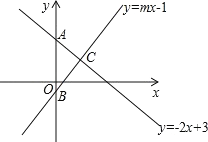
【题目】如图,直线y1=-2x+3和直线y2=mx-3分别交y轴于点A、B ,两直线交于点C(1,n).
(1)求 m、n 的值;
(2)求△ABC的面积;
(3)请根据图象直接写出:当 y1<y2时,自变量 x 的取值范围.
参考答案:
【答案】(1)m=4;(2)3;(3)当 x>1 时,y1<y2.
【解析】
(1)先把C(1,n)代入y1=-2x+3可求出n的值,从而确定C点坐标,然后把C点坐标代入入y2=mx-3即可求出m的值;
(2)先确定A点和B点坐标,然后根据三角形面积公式求解;
(3)观察函数图象得到当x>1时,直线y2=mx-3都在直线y1=-2x+3的上方.
(1)把 C(1,n)代入 y1=﹣2x+3 得 n=﹣2+3=1, 所以 C 点坐标为(1,1),
把 C(1,1)代入 y2=mx﹣3 得 m﹣3=1,解得 m=4;
(2)当 x=0 时,y=﹣2x+3=3,则 A(0,3); 当 x=0 时,y=4x﹣3=﹣3,则 B(0,﹣3),
所以△ABC 的面积=![]() ×(3+3)×1=3;
×(3+3)×1=3;
(3)当 x>1 时,y1<y2.
-
科目: 来源: 题型:
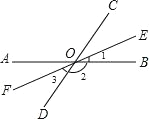
查看答案和解析>>【题目】如图,直线 AB、CD 相交于 O,∠BOC=70°,OE 是∠BOC 的角平分线,OF是OE的反向延长线.
(1)求∠1,∠2,∠3 的度数;
(2)判断 OF 是否平分∠AOD,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸上的每个小方格都是边长为1的正方形,△ABC 的顶点均在格点上,若 B
点的坐标为(-4,-2), 按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点A和点C的坐标;
(3)画出△ABC关于x轴的对称图形△ABC;
(4)△ABC 的面积为________.

-
科目: 来源: 题型:
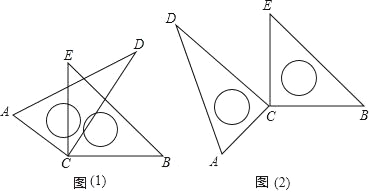
查看答案和解析>>【题目】数学活动课上,小聪同学摆弄着自己刚购买的一套三角板,将两块直角三角板的直角顶点C叠放在一起,然后转动三角板,在转动过程中,请解决以下问题:
(1)如图(1):当∠DCE=30°时,∠ACB+∠DCE= ,若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.
(2)当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的对应点如图所示.

(1)在横线上填上“>”或“=”或“<”:
a 0,a-b 0,
 .
.(2)在数轴上标出表示有理数-a,-b,-c的点;
(3)用“>”把a,b,c,-a,-b,-c连接起来.
-
科目: 来源: 题型:
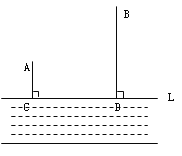
查看答案和解析>>【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车以汽车站为出发点,在东西方向的城市道路上进行营运,若规定向东为正,向西为负,行车依先后顺序记录如下(单位:千米):
+4,-5,+9,-3,+6,-3,-8,-4,+7,-6.
(1)计算说明出租车将最后一名乘客送到目的地,此时离汽车站多远?在汽车站什么方向?
(2)若该出租车每千米收费标准为3元,求出租车的营业额是多少元?
相关试题

