【题目】已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,

(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
参考答案:
【答案】见解析
【解析】试题分析:(1)先证得△ADB≌△CDB求得∠BCD=∠BAD,从而得到∠ADF=∠BAD,所以AB∥FD,因为BD⊥AC,AF⊥AC,所以AF∥BD,即可证得.
(2)先证得平行四边形是菱形,然后根据勾股定理即可求得.
试题解析:(1)证明:∵BD垂直平分AC,
∴AB=BC,AD=DC,
在△ADB与△CDB中,
 ,
,
∴△ADB≌△CDB(SSS)
∴∠BCD=∠BAD,
∵∠BCD=∠ADF,
∴∠BAD=∠ADF,
∴AB∥FD,
∵BD⊥AC,AF⊥AC,
∴AF∥BD,
∴四边形ABDF是平行四边形,
(2)解:∵四边形ABDF是平行四边形,AF=DF=5,
∴ABDF是菱形,
∴AB=BD=5,
∵AD=6,
设BE=x,则DE=5-x,
∴AB2-BE2=AD2-DE2,
即52-x2=62-(5-x)2
解得:x=![]() ,
,
∴![]() ,
,
∴AC=2AE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=
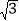 MN.
MN.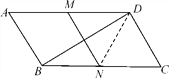
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生毕业后就读普通高中或就读中等职业技术学校的意向,某校对八、九年级部分学生进行了一次调查,调查结果有三种情况:
 只愿意就读普通高中;
只愿意就读普通高中; 只愿意就读中等职业技术学校;
只愿意就读中等职业技术学校; 就读普通高中或中等职业技术学校都愿意
就读普通高中或中等职业技术学校都愿意 学校教务处将调查数据进行了整理,并绘制了尚不完整的统计图如下,请根据相关信息,解答下列问题:
学校教务处将调查数据进行了整理,并绘制了尚不完整的统计图如下,请根据相关信息,解答下列问题: 本次活动一共调查的学生数为______名;
本次活动一共调查的学生数为______名; 补全图一,并求出图二中A区域的圆心角的度数;
补全图一,并求出图二中A区域的圆心角的度数; 若该校八、九年级学生共有2800名,请估计该校八、九年级学生只愿意就读中等职业技术学校的人数.
若该校八、九年级学生共有2800名,请估计该校八、九年级学生只愿意就读中等职业技术学校的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再解答问题
已知在平面内有两点 ,
, ,其两点间的距离公式为
,其两点间的距离公式为 ,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为
,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为 或
或
 已知点
已知点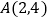 ,
, ,试求A,B两点间的距离;
,试求A,B两点间的距离; 已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为
已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为 ,试求A,B两点间的距离;
,试求A,B两点间的距离; 已知点
已知点 ,
, ,判断线段AB,BC,AC中哪两条是相等的?并说明理由.
,判断线段AB,BC,AC中哪两条是相等的?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】分别以□ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,AB是直径,AC是切线且AC=AB,联结BC交⊙O于点D,试仅用无刻度直尺,作以D为切点的⊙O的切线DT.

相关试题

