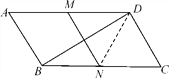
【题目】如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=![]() MN.
MN.
参考答案:
【答案】见解析
【解析】试题分析:(1)要证明四边形MNCD是平行四边形,即要证明MD=NC,MD∥NC,由四边形ABCD是平行四边形可得AD=BC,AD∥BC,又因为M、N分别是AD、BC的中点,所以MD=NC,MD∥NC;(2)连结ND,由四边形MNCD是平行四边形可得 MN=DC,因为N是BC的中点,所以BN=CN,结合BC=2CD,∠C=60°可以得出△NCD是等边三角形,进而得出ND=NC,∠DNC=60°,由三角形外角的性质可得∠NBD+∠NDB=∠DNC,
因为DN=NC=NB,所以∠DBN=∠BDN=![]() ∠DNC=30°,所以∠BDC=90°,最后结合tan∠DBC可证明DB=
∠DNC=30°,所以∠BDC=90°,最后结合tan∠DBC可证明DB=![]() MN.
MN.
试题解析:
(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,
∵M、N分别是AD、BC的中点,∴MD=NC,MD∥NC,
∴四边形MNCD是平行四边形;
(2)连结ND,
∵四边形MNCD是平行四边形,∴MN=DC,
∵N是BC的中点,∴BN=CN,
∵BC=2CD,∠C=60°,∴△NCD是等边三角形,∴ND=NC,∠DNC=60°,
∵∠DNC是△BND的外角,∴∠NBD+∠NDB=∠DNC,
∵DN=NC=NB,∴∠DBN=∠BDN=![]() ∠DNC=30°,∴∠BDC=90°,
∠DNC=30°,∴∠BDC=90°,
∵tan∠DBC=tan30°=![]() =
=![]() ,
,
∴DB=![]() DC=
DC=![]() MN.
MN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=
 x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并将不等式组的解集在数轴上表示出来.
,并将不等式组的解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生毕业后就读普通高中或就读中等职业技术学校的意向,某校对八、九年级部分学生进行了一次调查,调查结果有三种情况:
 只愿意就读普通高中;
只愿意就读普通高中; 只愿意就读中等职业技术学校;
只愿意就读中等职业技术学校; 就读普通高中或中等职业技术学校都愿意
就读普通高中或中等职业技术学校都愿意 学校教务处将调查数据进行了整理,并绘制了尚不完整的统计图如下,请根据相关信息,解答下列问题:
学校教务处将调查数据进行了整理,并绘制了尚不完整的统计图如下,请根据相关信息,解答下列问题: 本次活动一共调查的学生数为______名;
本次活动一共调查的学生数为______名; 补全图一,并求出图二中A区域的圆心角的度数;
补全图一,并求出图二中A区域的圆心角的度数; 若该校八、九年级学生共有2800名,请估计该校八、九年级学生只愿意就读中等职业技术学校的人数.
若该校八、九年级学生共有2800名,请估计该校八、九年级学生只愿意就读中等职业技术学校的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,

(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再解答问题
已知在平面内有两点 ,
, ,其两点间的距离公式为
,其两点间的距离公式为 ,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为
,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为 或
或
 已知点
已知点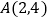 ,
, ,试求A,B两点间的距离;
,试求A,B两点间的距离; 已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为
已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为 ,试求A,B两点间的距离;
,试求A,B两点间的距离; 已知点
已知点 ,
, ,判断线段AB,BC,AC中哪两条是相等的?并说明理由.
,判断线段AB,BC,AC中哪两条是相等的?并说明理由.
相关试题

