【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0其中正确的是( ).

A. ①②③④ B. ①②④ C. ①③④ D. ①②③
参考答案:
【答案】D
【解析】由抛物线开口方向得到a>0,然后利用抛物线抛物线的对称轴得到b的符合,则可对①进行判断;利用判别式的意义和抛物线与x轴有2个交点可对②进行判断;利用x=1时,y<0和c<0可对③进行判断;利用抛物线的对称轴方程得到b=-2a,加上x=-1时,y>0,即a-b+c>0,则可对④进行判断.
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-![]() =1,
=1,
∴b=-2a<0,
∴ab<0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,所以②正确;
∵x=1时,y<0,
∴a+b+c<0,
而c<0,
∴a+b+2c<0,所以③正确;
∵抛物线的对称轴为直线x=-![]() =1,
=1,
∴b=-2a,
而x=-1时,y>0,即a-b+c>0,
∴a+2a+c>0,所以④错误.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们环保意识的不断增强,我市家庭电动自行车的拥有量逐年增加.据统计,某小区2014年底拥有家庭电动自行车125辆,2016年底家庭电动自行车的拥有量达到180辆.
(1)若该小区2014年底到2017年底家庭电动自行车拥有量的年平均增长率相同,则该小区到2017年底电动自行车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资3万元再建若干个停车位,据测算,建造费用分别为室内车位1000元/个,露天车位200元/个.考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,则该小区最多可建两种车位各多少个?试写出所有可能的方案.
-
科目: 来源: 题型:
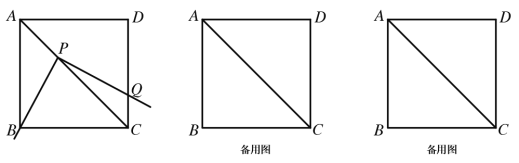
查看答案和解析>>【题目】将一把三角尺放在边长为2的正方形ABCD上(正方形四个内角为90°,四边都相等),并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC交于点Q。
探究:(1)当点Q在边CD 上时,线段PQ 与线段PB之间有怎样的大小关系?试证明你观察得到结论;
(2)当点Q在边CD 上时,如果四边形 PBCQ 的面积为1,求AP长度;
(3)当点P在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q的位置,并求出相应的AP的长;如果不可能,试说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A、B.
(1)求抛物线的解析式; (2)画出抛物线的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.
(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?
(2)若要使商场平均每天的盈利最多,每件衬衣应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图在直角坐标系中,点A在y轴上,BC⊥x轴于点C,点A关于直线OB的对称点D恰好在BC上,点E与点O关于直线BC对称,∠OBC=35°,则∠OED的度数为( )
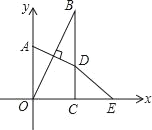
A.10°B.20°C.30°D.35°
相关试题

