【题目】如图,已知△ABC是等边三角形,D是AB边上任意一点,∠CDE=60°,DE与∠ABC外角平分线相交于点E.
(1)求证:CD=DE;

(2)若D是AB延长线上任意一点,∠CDE=60°,DE与∠ABC外角平分线相交于点E.请画出图形,判断CD=DE是否还成立?若成立,请给予证明;若不成立,请说明理由.

参考答案:
【答案】(1)证明见解析;(2)成立,证明见解析.
【解析】
(1)过点D作DF//BC,交AC于F,由等边三角形的性质可得AF=AD,进而可得CF=BD,根据外角性质可知∠FCD+∠CDF=60°,由∠CDE=60°,∠ADF=60°可得∠CDF+∠EDB=60°,进而可得∠FCD=∠EDB,由BE是外角平分线可得∠CBE=60°,即可证明∠DBE=∠CFD=120°,即可证明△CFD≌△DEB,进而可得CD=DE;(2)过点D作DP//BC,交AC延长线于点P,由等边三角形及平行线性质可得CP=BD,根据外角性质可得∠PCD=∠A+∠ADC=60°+∠ADC,由∠BDE=∠CDE+∠ADC=60°+∠ADC可证明∠PCD=∠BDE,根据BE是外角平分线可得∠EBD=∠P=60°,即可证明△PCD≌△BDE,进而可得CD=DE.
(1)如图,过点D作DF//BC,交AC于F,
∵△ABC是等边三角形,DF//BC,
∴CF=BD,∠AFD=60°,
∴∠CFD=180°-60°=120°,
∵DE是外角平分线,
∴∠CBE=60°,
∴∠DBE=120°,
∴∠CFD=∠DBE,
∵∠FCD+∠CDF=∠AFD=60°,∠BDE+∠CDF=180°-∠ADF-∠CDE=180°-60°-60°=60°,
∴∠FCD=∠BDE,
∴△CFD≌△DEB,
∴CD=DE.

(2)过点D作DP//BC,交AC延长线于点P,
∵△ABC是等边三角形,DP//BC,
∴PC=BD,∠P=60°,
∵BE是外角平分线,
∴∠DBE=60°,
∴∠DBE=∠P,
∵∠PCD=∠A+∠ADC=60°+∠ADC,∠BDE=∠ADC+∠CDE=60°+∠ADC,
∴∠PCD=∠BDE,
∴△PCD≌△BDE,
∴CD=DE

-
科目: 来源: 题型:
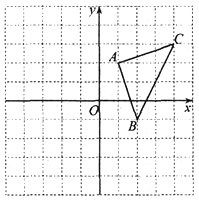
查看答案和解析>>【题目】如图,平面直角坐标系中,△ABC的顶点坐标为:A(1,2),B(2, 一1), C (4, 3).
(1)将△ABC向左平移2个单位长度,再向上平移1个单位长度,得△A'B'C'.画出△A'B'C',并写出△A'B'C'的顶点坐标;
(2)求△ABC的面积.
-
科目: 来源: 题型:
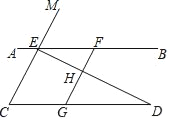
查看答案和解析>>【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和直线BC相交于点B,连接AC,点D、E、H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°.
(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=
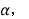 求∠3的度数(用含
求∠3的度数(用含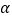 的代数式表示).
的代数式表示).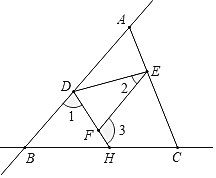
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
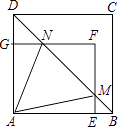
(1)求证: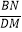 =
= 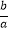 ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,A
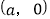 ,C
,C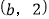 ,且满足
,且满足 过点C作CB⊥
过点C作CB⊥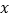 轴于点B.
轴于点B.(1)
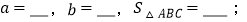
(2)在
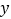 轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出点P的坐标;若不存在,请说明理由;
轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出点P的坐标;若不存在,请说明理由;(3)如图②,若过点B作BD∥AC交
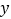 轴于点D,且AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.
轴于点D,且AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.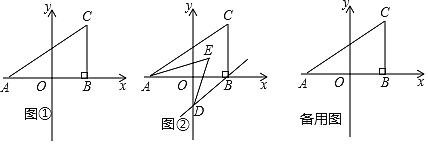
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2 , 请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
相关试题

