【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).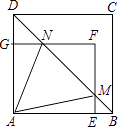
(1)求证: ![]() =
= ![]() ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.
参考答案:
【答案】
(1)证明:过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,
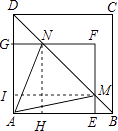
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°,
∴△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,
∴BN= ![]() NH=
NH= ![]() AG=
AG= ![]() b,DM=
b,DM= ![]() MI=
MI= ![]() AE=
AE= ![]() a,
a,
∴ ![]() =
= ![]()
(2)解:S△AMN=S△ABD﹣S△ABM﹣S△ADN
= ![]() ABAD﹣
ABAD﹣ ![]() ABME﹣
ABME﹣ ![]() ADNG
ADNG
= ![]() c2﹣
c2﹣ ![]() c(c﹣a)﹣
c(c﹣a)﹣ ![]() c(c﹣b)
c(c﹣b)
= ![]() c(c﹣c+a﹣c+b)
c(c﹣c+a﹣c+b)
= ![]() c(a+b﹣c)
c(a+b﹣c)
(3)解:∵∠DMA=∠ABD+∠MAB=∠MAB+45°,∠BAN=∠MAB+∠MAN=∠MAB+45°,
∴∠DMA=∠BAN,
∵∠ABD=∠ADB=45°,
∴△ADM∽△NBA,
∴ ![]() =
= ![]() ,
,
∵DM= ![]() a,BN=
a,BN= ![]() b,
b,
∴c2=2ab.
【解析】(1)作NH⊥AB垂足为H,作MI⊥AD垂足为I,依据题意可得到△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,则可求得BN=![]() b,DM=
b,DM=![]() a,最后,代入计算即可;
a,最后,代入计算即可;
(2)依据图形可知S△AMN=S△ABD-S△ABM-S△ADN,故此可得到S△AMN=![]() c2-
c2-![]() c(c-a)-
c(c-a)-![]() c(c-b),最后进行整理即可;
c(c-b),最后进行整理即可;
(3)首先证明∠DMA=∠BAN,然后再由∠ABD=∠ADB=45°可得到△ADM∽△NBA,最后,依据相似三角形的性质列出比例式求解即可.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
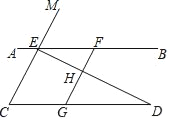
查看答案和解析>>【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和直线BC相交于点B,连接AC,点D、E、H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°.
(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=
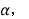 求∠3的度数(用含
求∠3的度数(用含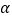 的代数式表示).
的代数式表示).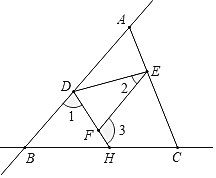
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,D是AB边上任意一点,∠CDE=60°,DE与∠ABC外角平分线相交于点E.
(1)求证:CD=DE;

(2)若D是AB延长线上任意一点,∠CDE=60°,DE与∠ABC外角平分线相交于点E.请画出图形,判断CD=DE是否还成立?若成立,请给予证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,A
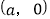 ,C
,C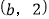 ,且满足
,且满足 过点C作CB⊥
过点C作CB⊥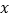 轴于点B.
轴于点B.(1)
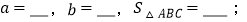
(2)在
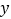 轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出点P的坐标;若不存在,请说明理由;
轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出点P的坐标;若不存在,请说明理由;(3)如图②,若过点B作BD∥AC交
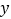 轴于点D,且AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.
轴于点D,且AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.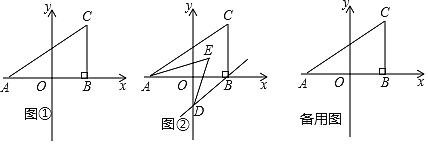
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2 , 请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】数据x1,x2,…,xn的方差为A,则数据3x1+1,3x2+1,…3xn+1的方差为( )
A. 3A B. 3A+1 C. 9A D. 9A+1
相关试题

