【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y= ![]() (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
参考答案:
【答案】
(1)
解:把A(﹣2,0)代入y=ax+1中,求得a= ![]() ,
,
∴y= ![]() x+1,
x+1,
由PC=2,把y=2代入y= ![]() x+1中,得x=2,即P(2,2),
x+1中,得x=2,即P(2,2),
把P代入y= ![]() 得:k=4,
得:k=4,
则双曲线解析式为y= ![]() ;
;
(2)
解:设Q(a,b),
∵Q(a,b)在y= ![]() 上,
上,
∴b= ![]() ,
,
当△QCH∽△BAO时,可得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴a﹣2=2b,即a﹣2= ![]() ,
,
解得:a=4或a=﹣2(舍去),
∴Q(4,1);
当△QCH∽△ABO时,可得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
整理得:2a﹣4= ![]() ,
,
解得:a=1+ ![]() 或a=1﹣
或a=1﹣ ![]() (舍),
(舍),
∴Q(1+ ![]() ,2
,2 ![]() ﹣2).
﹣2).
综上,Q(4,1)或Q(1+ ![]() ,2
,2 ![]() ﹣2).
﹣2).
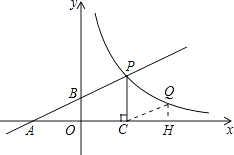
【解析】(1)把A坐标代入直线解析式求出a的值,确定出直线解析式,把y=2代入直线解析式求出x的值,确定出P坐标,代入反比例解析式求出k的值,即可确定出双曲线解析式;(2)设Q(a,b),代入反比例解析式得到b= ![]() ,分两种情况考虑:当△QCH∽△BAO时;当△QCH∽△ABO时,由相似得比例求出a的值,进而确定出b的值,即可得出Q坐标.
,分两种情况考虑:当△QCH∽△BAO时;当△QCH∽△ABO时,由相似得比例求出a的值,进而确定出b的值,即可得出Q坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=x﹣2与反比例函数y=
 的图象交于A、B两点.
的图象交于A、B两点. 
(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
组别
分组
频数
频率
1
50≤x<60
9
0.18
2
60≤x<70
a
3
70≤x<80
20
0.40
4
80≤x<90
0.08
5
90≤x≤100
2
b
合计

请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a、b、x、y的值;
(2)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B) -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品批发部准备用10000元从厂家购进一批出厂价分别为16元和20元的甲、乙两种酸奶,然后将甲、乙两种酸奶分别加价20%和25%向外销售.如果设购进甲种酸奶为x(箱),全部售出这批酸奶所获销售利润为y(元).
(1)求所获销售利润y(元)与x(箱)之间的函数关系式;
(2)根据市场调查,甲、乙两种酸奶在保质期内销售量都不超过300箱,那么食品批发部怎样进货获利最大,最大销售利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求代数式(
 ﹣
﹣  )÷
)÷  的值,其中x=2sin60°﹣1,y=tan45°.
的值,其中x=2sin60°﹣1,y=tan45°. -
科目: 来源: 题型:
查看答案和解析>>【题目】在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
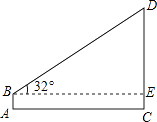
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张.

(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
相关试题

