【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张. 
(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
参考答案:
【答案】
(1)解:画树状图为:

共有12种等可能的结果数;
(2)解:抽到的两张卡片上的数都是勾股数的结果数为6,
所以抽到的两张卡片上的数都是勾股数的概率= ![]() =
= ![]() .
.
【解析】(1)利用树状图展示12种等可能的结果数;(2)根据勾股数可判定只有A卡片上的三个数不是勾股数,则可从12种等可能的结果数中找出抽到的两张卡片上的数都是勾股数的结果数,然后根据概率公式求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=
 (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求代数式(
 ﹣
﹣  )÷
)÷  的值,其中x=2sin60°﹣1,y=tan45°.
的值,其中x=2sin60°﹣1,y=tan45°. -
科目: 来源: 题型:
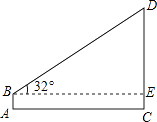
查看答案和解析>>【题目】在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
-
科目: 来源: 题型:
查看答案和解析>>【题目】六一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
(1)求A、B两种品牌服装每套进价分别为多少元?
(2)该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB、CD为⊙O的直径,弦BE交CD于点F,连接DE交AB于点G,GO=GD.
(1)如图1,求证:DE=DF;
(2)如图2,作弦AK∥DC,AK交BE于点N,连接CK,求证:四边形KNFC为平行四边形;
(3)如图3,作弦CH,连接DH,∠CDH=3∠EDH,CH=2 ,BE=4
,BE=4  ,求DH的长.
,求DH的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=a(x+1)2﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,﹣
 ),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧.
),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧.
(1)求a的值及点A,B的坐标;
(2)当直线l将四边形ABCD分为面积比为3:7的两部分时,求直线l的函数表达式;
(3)当点P位于第二象限时,设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.
相关试题

