【题目】某食品批发部准备用10000元从厂家购进一批出厂价分别为16元和20元的甲、乙两种酸奶,然后将甲、乙两种酸奶分别加价20%和25%向外销售.如果设购进甲种酸奶为x(箱),全部售出这批酸奶所获销售利润为y(元).
(1)求所获销售利润y(元)与x(箱)之间的函数关系式;
(2)根据市场调查,甲、乙两种酸奶在保质期内销售量都不超过300箱,那么食品批发部怎样进货获利最大,最大销售利润是多少?
参考答案:
【答案】
(1)解:根据题意,得:y=16x20%+(10000﹣16x)25%=﹣0.8x+2500;
(2)解:由题意知,  ,
,
解得250≤x≤300,
由(1)知y=﹣0.8x+2500,
∵k=﹣0.8<0,
∴y随x的增大而减小
∴当x=250时,y值最大,此时y=﹣0.8×250+2500=2300(元)
∴ ![]() =
= ![]() =300(箱).
=300(箱).
答:当购进甲种酸奶250箱,乙种酸奶300箱时,所获销售利润最大,最大销售利润为2300元.
【解析】(1)本题的等量关系是销售利润=购甲种酸奶的费用×20%+购乙种酸奶的费用×25%.可根据此等量关系得出y与x的函数关系式;(2)可根据“甲、乙两种酸奶在保质期内销售量都不超过300箱”,先求出自变量的取值范围,然后根据(1)中得出的函数的性质和自变量的取值范围,求出利润最大的方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半小时后返回A地.如图是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象.

(1)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=x﹣2与反比例函数y=
 的图象交于A、B两点.
的图象交于A、B两点. 
(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
组别
分组
频数
频率
1
50≤x<60
9
0.18
2
60≤x<70
a
3
70≤x<80
20
0.40
4
80≤x<90
0.08
5
90≤x≤100
2
b
合计

请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a、b、x、y的值;
(2)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=
 (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求代数式(
 ﹣
﹣  )÷
)÷  的值,其中x=2sin60°﹣1,y=tan45°.
的值,其中x=2sin60°﹣1,y=tan45°. -
科目: 来源: 题型:
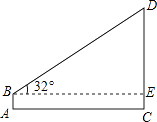
查看答案和解析>>【题目】在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
相关试题

