【题目】如图,△ABC看,∠BAC=90°,AC=12,AB=10,D是AC上一个动点,以AD为直径的⊙O交BD于E,则线段CE的最小值是( )

A. 5 B. 6 C. 7 D. 8
参考答案:
【答案】D
【解析】
连接AE,可得∠AED=∠BEA=90°,从而知点E在以AB为直径的⊙Q上,继而知点Q、E、C三点共线时CE最小,根据勾股定理求得QC的长,即可得线段CE的最小值.
如图,连接AE,则∠AED=∠BEA=90°,
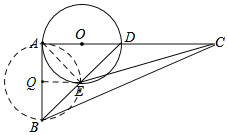
∴点E在以AB为直径的⊙Q上,
∵AB=10,
∴QA=QB=5,
当点Q、E、C三点共线时,QE+CE=CQ(最短),
而QE长度不变,故此时CE最小,
∵AC=12,
∴QC=![]() =13,
=13,
∴CE=QC-QE=13-5=8.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示的是嘉淇爸爸给嘉淇出的一道题,如图2所示的是嘉淇对该题的解答.她所写的结论中,正确的个数是( )
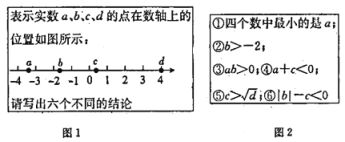
A.6B.5C.4D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AC=2,BC=4,CD=BD=DE,则CE=( )
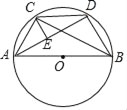
A. 3﹣
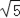 B.
B. 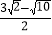 C.
C. 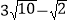 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连结EF,则线段EF长度的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题的大意是:有一块三角形沙田,三条边长分别为5里;12里;13里,问这块沙田面积有多大?题中的1里=0.5千米,则该沙田的面积为( )
A.3平方千米B.7.5平方千米C.15平方千米D.30平方千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
 ,
, ,
, ,
, ,…,则第8个等式是__________.
,…,则第8个等式是__________.
相关试题

