【题目】如图,在△ABC中,∠ACB= ![]() ,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.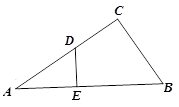
(1)求 ![]() 的值;
的值;
(2)当 ![]() 时,求
时,求 ![]() 的长.
的长.
参考答案:
【答案】
(1)解:解法一:∵DE⊥AB,
∴∠DEA=90°.
∴∠A+∠ADE=90°.
∵∠ACB= ![]() ,
,
∴∠A+∠B=90°.
∴∠ADE=∠B.
在Rt△ABC中,∵AC=12,BC=5,
∴AB=13.
∴ ![]() .
.
∴ ![]()
解法二:∵ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴△ ![]() ∽△
∽△ ![]() .
.
∴ ![]() .
.
在Rt△ ![]() 中,∵
中,∵ ![]() ,
,
∴ ![]()
∴ ![]()
∴ ![]()
(2)解:解法一:由(1)得 ![]() ,
,
设 ![]() 为
为 ![]() ,则
,则 ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
解得 ![]() .
.
∴ ![]() .
.
解法二:由(1)可知 △ ![]() ∽△
∽△ ![]() .
.
∴ ![]()
设 ![]() ,则
,则 ![]() .
.
∴ ![]() .
.
解得 ![]() .
.
∴ ![]() .
.
【解析】(1)根据勾股定理求出AB的值,根据同角的余角相等,得到∠ADE=∠B,根据三角函数的定义求出cos∠ADE的值;(2)根据三角函数值直接求出AD的值即可.
【考点精析】利用锐角三角函数的定义和同角三角函数的关系(倒数、平方和商)对题目进行判断即可得到答案,需要熟知锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数;各锐角三角函数之间的关系:平方关系(sin2A+cos2A=1);倒数关系(tanAtan(90°—A)=1);弦切关系(tanA=sinA/cosA ).
-
科目: 来源: 题型:
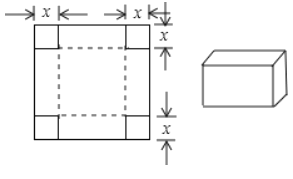
查看答案和解析>>【题目】如图所示,一张边长为
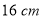 的正方形硬纸板,把它的四个角都剪去一个边长为工
的正方形硬纸板,把它的四个角都剪去一个边长为工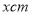 (
(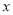 为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为
为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为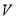 ,请回答下列问题:
,请回答下列问题:(1)用含有
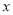 的代数式表示
的代数式表示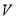 ,则
,则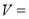
(2)完成下表:
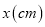
1
2
3
4
5
6
7
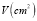
(3)观察上表,当
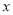 取什么值时,容积
取什么值时,容积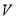 的值最大?
的值最大? -
科目: 来源: 题型:
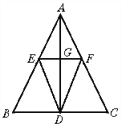
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.
(1)试说明△AEF是等腰三角形;
(2)试比较DE与DF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(—3,—3),B(—2,—1),C(—1,—2)是直角坐标平面上三点。

(1)请画出ΔABC关于原点O对称的ΔA1B1C1,
(2)请写出点B关天y轴对称的点B2的坐标,若将点B2向上平移h个单位,使其落在ΔA1B1C1内部,指出h的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( )
A. 在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形
B. 在△ABC中,若∠A∶∠B∶∠C=5∶2∶3,则△ABC为直角三角形
C. 在△ABC中,若a=
 c,b=
c,b= c,则△ABC为直角三角形
c,则△ABC为直角三角形D. 在△ABC中,若a∶b∶c=2∶2∶4,则△ABC为直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个等腰直角三角形按图示方式依次翻折,则下列说法正确的个数有( )

①DF平分∠BDE;②△BFD是等腰三角形;;③△CED的周长等于BC的长.
A. 0个; B. 1个; C. 2个; D. 3个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.
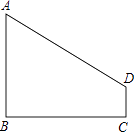
(1)求线段AD的长.
(2)在线段BC上是否存在点P,使△APD是等腰三角形?若存在,求出线段BP的长;若不存在,请说明理由.
相关试题

