【题目】如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.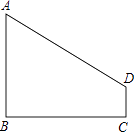
(1)求线段AD的长.
(2)在线段BC上是否存在点P,使△APD是等腰三角形?若存在,求出线段BP的长;若不存在,请说明理由.
参考答案:
【答案】
(1)解:如图1,过D作DE⊥AB于E点,
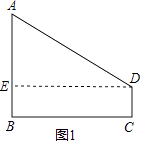
AE=4﹣1=3,DE=BC=4,
在Rt△AED中,AD= ![]() =5;
=5;
(2)解:如图2,
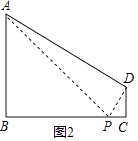
当AP=AD时,
在Rt△ABP中,BP= ![]() =3;
=3;
如图3,

当PA=PD时,
AB2+BP2=CD2+(BC﹣BP)2,即42+BP2=12+(4﹣BP)2,
解得BP= ![]() .
.
综上所述,线段BP的长是3或 ![]() .
.
【解析】(1)根据已知可知四边形ABCD是梯形,要解决梯形的问题通过作高,转化到直角三角形中解决。因此过D作DE⊥AB于E点,可证得BCDE是矩形,就可求出DE和AE的长,再根据勾股定理在Rt△AED中求出AD的长。
(2)根据题意可知,分两种情况,当AP=AD时,在Rt△ABP中,利用勾股定理求出BP的长;当PA=PD时,根据勾股定理,利用PA2=PD2,建立方程,求解即可。
【考点精析】通过灵活运用等腰三角形的判定和勾股定理的概念,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=
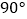 ,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.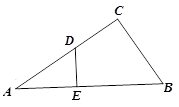
(1)求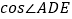 的值;
的值;
(2)当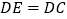 时,求
时,求 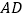 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( )
A. 在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形
B. 在△ABC中,若∠A∶∠B∶∠C=5∶2∶3,则△ABC为直角三角形
C. 在△ABC中,若a=
 c,b=
c,b= c,则△ABC为直角三角形
c,则△ABC为直角三角形D. 在△ABC中,若a∶b∶c=2∶2∶4,则△ABC为直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个等腰直角三角形按图示方式依次翻折,则下列说法正确的个数有( )

①DF平分∠BDE;②△BFD是等腰三角形;;③△CED的周长等于BC的长.
A. 0个; B. 1个; C. 2个; D. 3个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①是一个长为
 、宽为
、宽为 的长方形,沿图中虛线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿图中虛线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.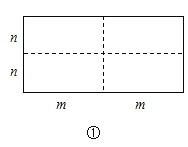
(1)图②中的阴影部分的面积为
(2)观察图②,请你写出代数式
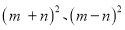 与
与 之间的等量关系式
之间的等量关系式 
(3)若
 则
则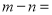
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示
(5)试画出一个几何图形,使它的面积能表示
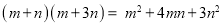
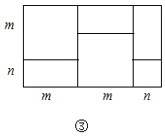
-
科目: 来源: 题型:
查看答案和解析>>【题目】在以“关爱学生、安全第一”为主题的安全教育宣传月活动中,某学校为了了解本校学生的上学方式,在全校范围内随机抽查部分学生,了解到上学方式主要有:A﹣﹣结伴步行、B﹣﹣自行乘车、C﹣﹣家人接送、D﹣﹣其它方式,并将收集的数据整理绘制成如下两幅不完整的统计图,请根据图中信息,解答下列问题:
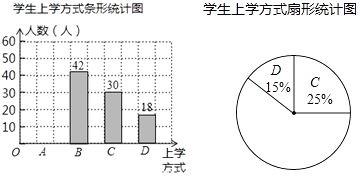
(1)本次抽查的学生人数是多少人?
(2)请补全条形统计图和扇形统计图,并在图中标出“自行乘车”对应扇形的圆心角的度数;
(3)如果该校学生有2080人,请你估计该校“家人接送”上学的学生约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】为支援四川抗震救灾,某省某市A、B、C三地分别有赈灾物资100吨、100吨、80吨,需要全部运往四川重灾区的甲、乙两县.根据灾区的情况,这批赈灾物资运往甲县的数量比运往乙县的数量的2倍少20吨.
(1)求这批赈灾物资运往甲、乙两县的数量各是多少吨?
(2)若要求C地运往甲县的赈灾物资为60吨,A地运往甲县的赈灾物资为x吨(x为整数),B地运往甲县的赈灾物资数量少于A地运往甲县的赈灾物资数量的2倍,其余的赈灾物资全部运往乙县,且B地运往乙县的赈灾物资数量不超过25吨.则A、B两地的赈灾物资运往甲、乙两县的方案有几种?
(3)已知A、B、C三地的赈灾物资运往甲、乙两县的费用如表:
A地
B地
C地
运往甲县的费用(元/吨)
220
200
200
运往乙县的费用(元/吨)
250
220
210
为及时将这批赈灾物资运往甲、乙两县,某公司主动承担运送这批物资的总费用,在(2)的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?
相关试题

