【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,![]() ,
,![]() ,且∠ABC=900.
,且∠ABC=900.
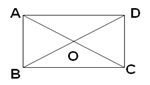
(1)求证:四边形ABCD是矩形.
(2)若∠ACB=300,AB=1,求①∠AOB的度数;②四边形ABCD的面积。
参考答案:
【答案】(1)见解析;(2)①60°,②![]() .
.
【解析】
(1)根据AO=CO,BO=DO可知四边形ABCD是平行四边形,又∠ABC=90°,可证四边形ABCD是矩形
(2)利用直角△ABC中∠ABC=90°,∠ACB=300,可得∠BAC=60°,AC=2,BC=![]() ,即可求得四边形ABCD的面积,同时利用矩形的性质,对角线相等且互相平分,可得∠AOB=180°-2∠BAC
,即可求得四边形ABCD的面积,同时利用矩形的性质,对角线相等且互相平分,可得∠AOB=180°-2∠BAC
解:(1)证明:∵AO=CO,BO=DO
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC=90°,
∴四边形ABCD是矩形;
(2)∵∠ABC=90°,∠ACB=300,AB=1
∴∠BAC=60°,AC=2,BC=![]()
又∵矩形ABCD中,OA=OB
∴∠AOB=180°-2∠BAC=60°
S□ABCD=1×![]() =
=![]()
-
科目: 来源: 题型:
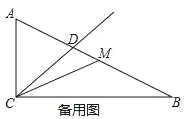
查看答案和解析>>【题目】如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.
(1)求线段CD的长;
(2)当点P在CD的延长线上,且∠PAB=45°时,求CP的长;
(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.

-
科目: 来源: 题型:
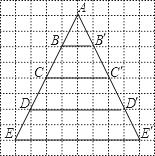
查看答案和解析>>【题目】如图,△ACC′是由△ABB′经过位似变换得到的
(1)求出△ACC′与△ABB′的相似比,并指出它们的位似中心;
(2)△AEE′是△ABB′的位似图形吗?如果是,求相似比;如果不是说明理由;
(3)如果相似比为3,那么△ABB′的位似图形是什么?
-
科目: 来源: 题型:
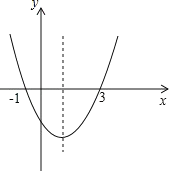
查看答案和解析>>【题目】如图,二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1,3,则:
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意 x 均有 ax2+bx≥a+b,其中结论正确的个数有( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L:
 与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),线段OA上的动点M(与O,A不重合)从A点以每秒1个单位的速度沿x轴向左移动。
与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),线段OA上的动点M(与O,A不重合)从A点以每秒1个单位的速度沿x轴向左移动。
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式,并写出t的取值范围;
(3)当t何值时△COM≌△AOB,并求此时M点的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)解下列不等式(组),并把它们的解集在数轴上表示出来;
(1)
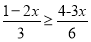 ; (2)
; (2)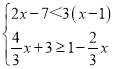
(Ⅱ)解方程组
(1)
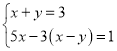 ; (2)
; (2)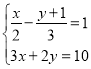 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O,以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B…依此类推,则平行四边形AO2019C2020B的面积为( )cm2.

A.
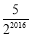 B.
B. 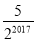 C.
C.  D.
D. 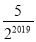
相关试题

