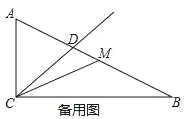
【题目】如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.
(1)求线段CD的长;
(2)当点P在CD的延长线上,且∠PAB=45°时,求CP的长;
(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)CP的长是
;(3)CP的长是![]() 或
或![]() 或
或![]() .
.
【解析】分析:(1)作辅助线,证明四边形ECFD是正方形,设DF=x,则CF=x,BF=2﹣x,由△BDF∽△BAC,得![]() ,可得CD的长;
,可得CD的长;
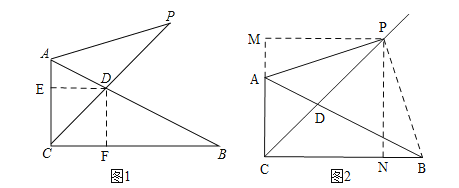
(2)如图2,作辅助线,构建全等三角形,先根据C、B、P、A四点共圆,得∠APB=90°,可知AP=BP,由角平分线性质得:PM=PN,根据HL证明Rt△PMA≌Rt△PNB(HL),得AM=BN,设AM=x,则PM=CM=x+1,CN=2﹣x,由CM=CN列方程可得x的值,可得CD的长;
(3)存在三种情况:
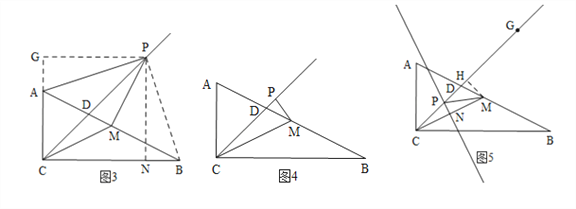
①当PM=CM时,如图3,同理作出辅助线,根据△PCM是等腰直角三角形,可得CP的长;
②先根据勾股定理求AB=![]() ,根据直角三角形斜边中线等于斜边一半可得CP的长;
,根据直角三角形斜边中线等于斜边一半可得CP的长;
③由△CPN∽△CMH,列比例式结合①可得CP的长.
详解:(1)如图1,过D作DE⊥AC于E,DF⊥BC于F.
∵DF平分∠ACB,∠ACB=90°,∴DE=DF.
∵∠DEC=∠ACB=∠CFD=90°,
∴四边形ECFD是正方形.
设DF=x,则CF=x,BF=2﹣x.
∵DF∥AC,∴△BDF∽△BAC,
∴![]() ,∴x=
,∴x=![]() .
.
∵△CDE是等腰直角三角形,∴CD=![]() ;
;
(2)如图2.∵∠PAB=∠PCB=45°,
∴C、B、P、A四点共圆,∴∠ACB+∠APB=180°.
∵∠ACB=90°,∴∠APB=90°,
∴△APB是等腰直角三角形,∴AP=BP.
过P作PM⊥AC于M,PN⊥BC于N,连接PB.
∵PM=PN,∴R△PMA≌Rt△PNB(HL),∴AM=BN.
由(1)知:四边形MCNP是正方形,∴CM=CN.
设AM=x,则PM=CM=x+1,CN=2﹣x,
∴x+1=2﹣x,x=![]() ,∴CM=
,∴CM=![]() ,∴CP=
,∴CP=![]() ;
;
(3)若△CMP是等腰三角形,存在三种情况:
①当PM=CM时,如图3,同理作出辅助线.
∵∠PCN=45°,∴△PCM是等腰直角三角形,∴CN=PN,
同(2)得:CP=![]() ;
;
②Rt△ACB中,AC=1,BC=2,∴AB=![]() .
.
∵M是AB的中点,∴CM=CP=![]() AB=
AB=![]() ;
;
③作CM的中垂线交CD于P,则CP=PM,过M作MH⊥CD于H.
由①知:CG(就是CP=![]() )=
)=![]() ,CH=
,CH=![]() .
.
∵△CPN∽△CMH,∴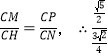 =
=![]() ,CP=
,CP=![]() .
.
综上所述:CP的长是![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
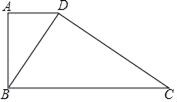
查看答案和解析>>【题目】已知四边形ABCD中,∠BAD=∠BDC=90°,BD2=ADBC.
(1)求证:AD∥BC;
(2)过点A作AE∥CD交BC于点E.请完善图形并求证:CD2=BEBC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有两个可以自由转动的均匀转盘A、B,转盘A被分为3等份,分别标有1、2、3三个数字;转盘B被分为4等份,分别标有3、4、5、6四个数字;有人为甲、乙两人设计了一个游戏规则:自由转动转盘A和B,转盘停止后,指针各指向一个数字(若指针恰好停在分界线上时,当作指向右边的数字),将指针所指的两个数字相加,如果和为6,那么甲获胜,否则乙获胜。

请你用概率的有关知识进行说明,这个游戏规则是否公平?如果不公平,那么谁获胜的可能性大些?
-
科目: 来源: 题型:
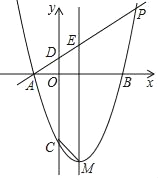
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.
(1)求点A的坐标和抛物线的表达式;
(2)当AE:EP=1:2时,求点E的坐标;
(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.
-
科目: 来源: 题型:
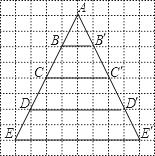
查看答案和解析>>【题目】如图,△ACC′是由△ABB′经过位似变换得到的
(1)求出△ACC′与△ABB′的相似比,并指出它们的位似中心;
(2)△AEE′是△ABB′的位似图形吗?如果是,求相似比;如果不是说明理由;
(3)如果相似比为3,那么△ABB′的位似图形是什么?
-
科目: 来源: 题型:
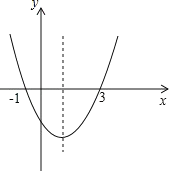
查看答案和解析>>【题目】如图,二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1,3,则:
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意 x 均有 ax2+bx≥a+b,其中结论正确的个数有( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,
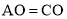 ,
,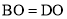 ,且∠ABC=900.
,且∠ABC=900.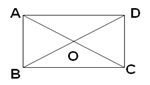
(1)求证:四边形ABCD是矩形.
(2)若∠ACB=300,AB=1,求①∠AOB的度数;②四边形ABCD的面积。
相关试题

