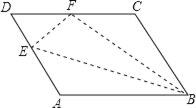
【题目】如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在边CD上的点F处,若△DEF的周长为8,△CBF的周长为18,则FC的长为_____.
参考答案:
【答案】5
【解析】
分析题意,△FBE为△ABE的翻折后的三角形,则△FBE≌△ABE,利用全等三角形各对应边相等、平行四边形的性质及线段间的等量关系可求解FC的长.
解:根据题意得△FBE≌△ABE,
∴EF=AE,BF=AB.
∵平行四边形ABCD,
∴AD=BC,AB=DC.
∵△FDE的周长为8,即DF+DE+EF=8,
∴DF+DE+AE=8,即DF+AD=8.
∵△FCB的周长为18,即FC+BC+BF=18,
∴FC+AD+DC=18,即2FC+AD+DF=18.
∴2FC+8=18,
∴FC=5.
故答案为:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )

A.164m
B.178m
C.200m
D.1618m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请认真阅读解题过程,在括号内填上相应的依据:

解:∵AD∥BC(已知),
∴∠1=∠3(________).
∵∠1=∠2(已知),
∴∠2=∠3(________).
∴BE∥DF(________).
∴∠3+∠4=180°(________).
-
科目: 来源: 题型:
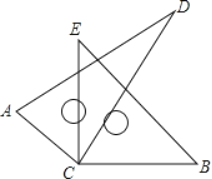
查看答案和解析>>【题目】如图,将两块直角三角板的直角顶点C叠放在一起.
(1)若∠DCE=28°10',求∠ACB的度数;
(2)若∠ACB=148°21',求∠DCE的度数;
(3)直接写出∠ACB与∠DCE的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图点A(1,1),B(2,﹣3),点P为x轴上一点,当|PA﹣PB|最大时,点P的坐标为( )

A. (﹣1,0) B. (
 ,0) C. (
,0) C. ( ,0) D. (1,0)
,0) D. (1,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为 n mile.(结果取整数,参考数据:
 ≈1.7,
≈1.7,  ≈1.4)
≈1.4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

相关试题

