【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

参考答案:
【答案】不能并排裁出两个面积均为147cm2的圆,理由见解析.
【解析】分析:根据长方形的长宽比设长方形的长DC为3xcm,宽AD为2xcm,结合长方形ABCD的面积为300cm![]() ,即可得出关于x的一元二次方程,解方程即可求出x的值,从而得出AB的长,再根据圆的面积公式以及圆的面积147cm
,即可得出关于x的一元二次方程,解方程即可求出x的值,从而得出AB的长,再根据圆的面积公式以及圆的面积147cm![]() ,即可求出圆的半径,从而可得出两个圆的直径的长度,将其与AB的长进行比较即可得出结论.
,即可求出圆的半径,从而可得出两个圆的直径的长度,将其与AB的长进行比较即可得出结论.
本题解析:设长方形的长DC为3xcm,宽AD为2xcm.
由题意,得 3x2x=300,
∵x>0,
∴![]() ,
,
∴AB=![]() cm,BC=
cm,BC=![]() cm.
cm.
∵圆的面积为147cm2,设圆的半径为rcm,
∴πr2=147,
解得:r=7cm.
∴两个圆的直径总长为28cm.
∵![]() ,
,
∴不能并排裁出两个面积均为147cm2的圆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市按以下规定收取每月的水费:用水不超过10立方米,按每立方米2.1元收费;如果超过10立方米,超过部分按每立方米3元收费,已知某用户l2月水费平均每立方米2.5元.
按要求回答下列问题:
(1)这个用户12月用水量10立方米(填“超过”或“不超过”).
(2)在(1)的前提下,求12月这个用户的用水量是多少立方米?
(3)该用户12月份需交水费元. -
科目: 来源: 题型:
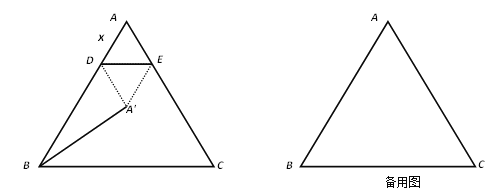
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=6,点D为AB边上的一动点(D不与A、B重合),过D作DE∥BC,交AC于点E.把△ADE沿直线DE折叠,点A落在点A'处.连结BA',设AD=x,△ADE的边DE上的高为y.
(1) 求出y与x的函数关系式;
(2) 若以点A'、B、D为顶点的三角形与△ABC 相似,求x的值;
(3) 当x取何值时,△A' DB是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是正方形,
是正方形, 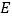 是
是 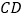 垂直平分线上的点,点
垂直平分线上的点,点 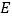 关于
关于 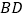 的对称点是
的对称点是 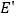 ,直线
,直线 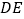 与直线
与直线 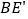 交于点
交于点 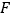 .
.
(1)若点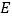 是
是 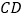 边的中点,连接
边的中点,连接 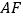 ,则
,则 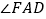 =;
=;
(2)小明从老师那里了解到,只要点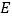 不在正方形的中心,则直线
不在正方形的中心,则直线 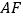 与
与 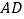 所夹锐角不变.他尝试改变点
所夹锐角不变.他尝试改变点 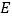 的位置,计算相应角度,验证老师的说法.
的位置,计算相应角度,验证老师的说法.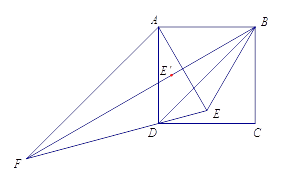
如图,将点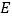 选在正方形内,且△
选在正方形内,且△ 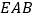 为等边三角形,求出直线
为等边三角形,求出直线 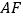 与
与 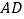 所夹锐角的度数;
所夹锐角的度数;
(3)请你继续研究这个问题,可以延续小明的想法,也可用其它方法.
我选择小明的想法;并简述求直线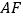 与
与 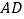 所夹锐角度数的思路.
所夹锐角度数的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于正数
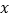 ,用符号
,用符号 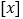 表示
表示 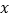 的整数部分,例如:
的整数部分,例如:  ,
,  ,
, 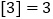 .点
.点 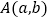 在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于
在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于 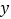 轴的边长为
轴的边长为 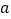 ,垂直于
,垂直于 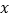 轴的边长为
轴的边长为 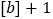 ,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点
,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点 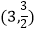 的矩形域是一个以
的矩形域是一个以 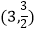 为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.
为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.

图1 图2
根据上面的定义,回答下列问题:
(1)在图2所示的坐标系中画出点 的矩形域,该矩形域的面积是;
(2)点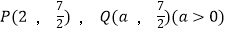 的矩形域重叠部分面积为1,求
的矩形域重叠部分面积为1,求 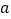 的值;
的值;
(3)已知点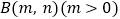 在直线
在直线  上, 且点B的矩形域的面积
上, 且点B的矩形域的面积  满足
满足 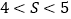 ,那么
,那么  的取值范围是 . (直接写出结果)
的取值范围是 . (直接写出结果)
相关试题

