Question

【题目】如图：在等腰直角三角形中，AB=AC，点D是斜边BC上的中点，点E、F分别为AB，AC上的点，且DE⊥DF．

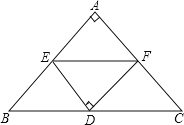
（1）若设BE=a，CF=b，满足+|b﹣5|=+，求BE及CF的长．

（2）求证：BE2+CF2=EF2．

（3）在（1）的条件下，求△DEF的面积．

Answer 1

【答案】（1）BE=12，CF=5；（2）见解析；（3）．

【解析】

试题分析：（1）先根据二次根式的非负性求出m=2，再由非负数的性质求出a、b的值，进而得到BE及CF的长；

（2）延长ED到P，使DP=DE，连接FP，CP，利用SAS得到三角形BED与三角形CPD全等，利用全等三角形对应边相等得到BE=CP，再利用SAS得到△EDF和△PDF全等，利用全等三角形对应边相等得到EF=FP，利用等角的余角相等得到∠FCP为直角，在直角三角形FCP中，利用勾股定理列出关系式，等量代换即可得证；

（3）连接AD，由AB=AC，且D为BC的中点，利用三线合一得到AD垂直于BC，AD为角平分线，再由三角形ABC为等腰直角三角形，得到一对角相等，利用同角的余角相等得到一对角相等，再由AD=CD，利用ASA得到三角形AED与三角形CFD全等，利用全等三角形对应边相等得到AE=CF=5，DE=DF，由AE+EB求出AB的长，即为AC的长，再由AC﹣CF求出AF的长，在直角三角形AEF中，利用勾股定理求出EF的长，再根据三角形DEF为等腰直角三角形求出DE与DF的长，即可确定出三角形DEF的面积．

（1）解：由题意得，

解得m=2，

则+|b﹣5|=0，

所以a﹣12=0，b﹣5=0，

a=12，b=5，

即BE=12，CF=5；

（2）证明：延长ED到P，使DP=DE，连接FP，CP，

在△BED和△CPD中，

，

∴△BED≌△CPD（SAS），

∴BE=CP，∠B=∠CDP，

在△EDF和△PDF中，

，

∴△EDF≌△PDF（SAS），

∴EF=FP，

∵∠B=∠DCP，∠A=90°，

∴∠B+∠ACB=90°，

∴∠ACB+∠DCP=90°，即∠FCP=90°，

在Rt△FCP中，根据勾股定理得：CF2+CP2=PF2，

∵BE=CP，PF=EF，

∴BE2+CF2=EF2；

（3）解：连接AD，

∵△ABC为等腰直角三角形，D为BC的中点，

∴∠BAD=∠FCD=45°，AD=BD=CD，AD⊥BC，

∵ED⊥FD，

∴∠EDA+∠ADF=90°，∠ADF+∠FDC=90°，

∴∠EDA=∠FDC，

在△AED和△CFD中，

，

∴△AED≌△CFD（ASA），

∴AE=CF=5，DE=DF，即△EDF为等腰直角三角形，

∴AB=AE+EB=5+12=17，

∴AF=AC﹣FC=AB﹣CF=17﹣5=12，

在Rt△EAF中，根据勾股定理得：EF==13，

设DE=DF=x，

根据勾股定理得：x2+x2=132，

解得：x=，即DE=DF=，

则S△DEF=DEDF=××=．