【题目】以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是 .
参考答案:
【答案】![]()
【解析】
解:
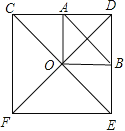
∵四边形CDEF是正方形,
∴∠OCD=∠ODB=45°,∠COD=90°,OC=OD,
∵AO⊥OB,
∴∠AOB=90°,
∴∠CAO+∠AOD=90°,∠AOD+∠DOB=90°,
∴∠COA=∠DOB,
∵在△COA和△DOB中
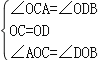 ,
,
∴△COA≌△DOB,
∴OA=OB,
∵∠AOB=90°,
∴△AOB是等腰直角三角形,
由勾股定理得:AB=![]() =
=![]() OA,
OA,
要使AB最小,只要OA取最小值即可,
根据垂线段最短,OA⊥CD时,OA最小,
∵正方形CDEF,
∴FC⊥CD,OD=OF,
∴CA=DA,
∴OA=![]() CF=1,
CF=1,
即AB=![]() ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论: ①abc<0;②b2﹣4ac>0;③3a+c>0;④(a+c)2<b2 ,
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
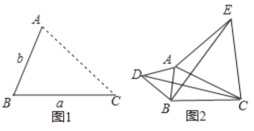
查看答案和解析>>【题目】(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.当点A位于什么上时,线段AC的长取得最大值,且最大值为多少(用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=4,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
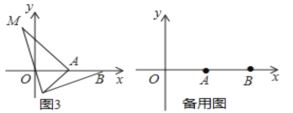
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(6,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD.若AD=4,BC=6,则梯形ABCD的面积是 .
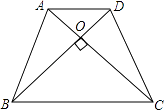
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2
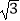 ,∠C=120°,以点C为圆心的
,∠C=120°,以点C为圆心的 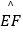 与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 .
与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 . 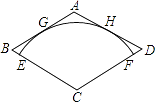
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD.若AD=4,BC=6,则梯形ABCD的面积是 .
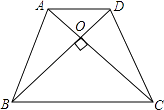
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2
 ,∠C=120°,以点C为圆心的
,∠C=120°,以点C为圆心的  与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 .
与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 . 
相关试题

