【题目】如图,在菱形ABCD中,AB=2 ![]() ,∠C=120°,以点C为圆心的
,∠C=120°,以点C为圆心的 ![]() 与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 .
与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 . 
参考答案:
【答案】2 ![]()
【解析】解:如图:连接CG, 
∵∠C=120°,
∴∠B=60°,
∵AB与 ![]() 相切,
相切,
∴CG⊥AB,
在直角△CBG中,CG=BCsin60°=2 ![]() ×
× ![]() =3,即圆锥的母线长是3,
=3,即圆锥的母线长是3,
设圆锥底面的半径为r,则:2πr= ![]() ,
,
∴r=1.
则圆锥的高是: ![]() =2
=2 ![]() .
.
所以答案是:2 ![]() .
.
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2
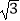 ,∠C=120°,以点C为圆心的
,∠C=120°,以点C为圆心的 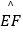 与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 .
与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 . 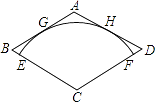
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD.若AD=4,BC=6,则梯形ABCD的面积是 .
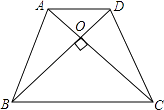
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF,求BE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算: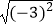 ﹣(
﹣(  )﹣1+(π﹣
)﹣1+(π﹣ 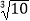 )0﹣(﹣1)100;
)0﹣(﹣1)100;
(2)已知|a+1|+(b﹣3)2=0,求代数式( ﹣
﹣ 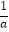 )÷
)÷ 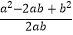 的值.
的值. -
科目: 来源: 题型:
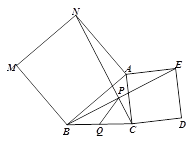
查看答案和解析>>【题目】探究:如图,分别以△ABC的两边AB和AC为边向外作正方形ABMN和正方形ACDE,CN、BE交于点P. 求证:∠ANC = ∠ABE.
应用:Q是线段BC的中点,连结PQ. 若BC = 6,则PQ = ___________.
相关试题

