【题目】在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,顶点在格点上的三角形叫做格点三角形,如格点三角形△ABC.
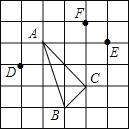
(1)△ABC的面积为 ;
(2)△ABC的形状为 ;
(3)根据图中标示的各点(A、B、C、D、E、F)位置,与△ABC全等的格点三角形是 .
参考答案:
【答案】(1)2;(2)直角三角形;(3)△DBC,△DAB,△DAC.
【解析】
(1)用三角形ABC所在的长方形的面积减去四周的三个三角形的面积即可得;
(2)利用勾股定理分别求出三角形ABC的边长,再利用勾股定理的逆定理进行判断即可;
(3)已知△ABC的各边长,根据网格的特征以及全等三角形的性质可得.
(1)△ABC的面积为:2×3﹣![]() ﹣
﹣![]() ﹣
﹣![]() =2,
=2,
故答案为:2;
(2)由勾股定理得:AC=![]() =2
=2![]() ,BC=
,BC=![]() =
=![]() ,AB=
,AB=![]() =
=![]() ,
,
所以AC2+BC2=AB2,
即∠ACB=90°,
即△ABC是直角三角形,
故答案为:直角三角形;
(3)与△ABC全等的格点三角形是△DBC,△DAB,△DAC,
故答案为:△DBC,△DAB,△DAC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为
 (千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与
(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与 之间的函数关系如图所示,折线OAB表示y乙与
之间的函数关系如图所示,折线OAB表示y乙与 之间的函数关系.
之间的函数关系.(1)甲采摘园的门票是 元,在乙园采摘草莓超过______
 后超过部分有打折优惠;
后超过部分有打折优惠;(2)当采摘量
 时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 为
为 的直径,
的直径, 、
、 为
为 的切线,
的切线, 、
、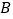 为切点,
为切点,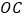 交
交 于点
于点 ,
, 的延长线交
的延长线交 于点
于点 ,连接
,连接 、
、 .给出以下结论:①
.给出以下结论:① ;②
;② ;③点
;③点 为
为 的内心.其中正确的是________(填序号).
的内心.其中正确的是________(填序号).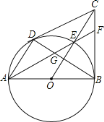
-
科目: 来源: 题型:
查看答案和解析>>【题目】海水养殖是莱州经济产业的亮丽名片之一,某养殖场响应山东省加快新旧动能转换的号召,今年采用新技术投资养殖了200万笼扇贝,并且全部被订购,已知每笼扇贝的成本是40元,售价是100元,打捞出售过程中发现,一部分扇贝生长情况不合要求,最后只能按照25元一笼出售,如果纯收入为
 万元,不合要求的扇贝有
万元,不合要求的扇贝有 万笼.
万笼.(1)求纯收入
 关于
关于 的关系式.
的关系式.(2)当
 为何值时,养殖场不赔不嫌?
为何值时,养殖场不赔不嫌? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数的图象过点
 .
. 求函数的解析式.
求函数的解析式. 随
随 的增大而如何变化?
的增大而如何变化? 点
点 ,
, 和
和 哪些点在图象上?
哪些点在图象上? 画出这个函数的图象.
画出这个函数的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
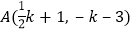 、
、 在反比例函数
在反比例函数 上,作等腰直角三角形
上,作等腰直角三角形 ,点
,点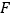 为斜边
为斜边 的中点,连
的中点,连 并延长交
并延长交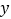 轴于点
轴于点 .
.
 求反比例函数的解析式;
求反比例函数的解析式; 的面积是多少?
的面积是多少? 若点
若点 在直线
在直线 上,请求出直线
上,请求出直线 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明为校合唱队购买某种服装时,商店经理给出了如下优惠条件:如果一次性购买不超过
 件,单价为
件,单价为 元;如果一次性购买多于
元;如果一次性购买多于 件,那么每增加
件,那么每增加 件,购买的所有服装的单价降低
件,购买的所有服装的单价降低 元,但单价不得低于
元,但单价不得低于 元.按此优惠条件,小明一次性购买这种服装
元.按此优惠条件,小明一次性购买这种服装 (
( 为正整数)件,支付
为正整数)件,支付 元.
元. 当
当 时,小明购买的这种服装的单价为________元;
时,小明购买的这种服装的单价为________元; 写出
写出 关于
关于 的函数表达式,并给出自变量
的函数表达式,并给出自变量 的取值范围;
的取值范围; 小明一次性购买这种服装付了
小明一次性购买这种服装付了 元,请问他购买了多少件这种服装?
元,请问他购买了多少件这种服装?
相关试题

