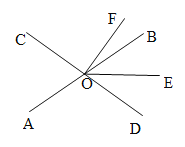
【题目】如图,直线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() 平分
平分![]() ,
,![]() ,设
,设![]() .
.
①求证![]() ;
;
②求![]() 的度数.
的度数.
参考答案:
【答案】(1)∠EOF=55°;(2)①证明见解析;②∠AOC=100°.
【解析】
(1)由对顶角及角平分线的定义即可计算得出;
(2)①由对顶角得出∠BOC=∠AOD再根据角平分线的定义即可得到∠BOE=∠DOE,两式相加即可;
②根据角度的运算及角平分线的定义,用x表达出∠BOF的度数,再解方程即可.
解:(1)∵直线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]()
∴∠BOD=∠AOC=70°,
∵![]() 平分
平分![]() ,
,
∴∠BOE=∠DOE=35°,
又∵![]() ,
,
∴∠EOF=∠DOF-DOE=90°-35°=55°.
(2)①∵直线![]() ,
,![]() 相交于点
相交于点![]() ,
,
∴∠BOC=∠AOD
又∵![]() 平分
平分![]() ,
,
∴∠BOE=∠DOE,
∴∠BOC+∠BOE=∠AOD+∠DOE
即![]()
②∵![]() ,
,![]() ,
,
∴∠COE=x°,
∴∠DOE=180°-x°
∵OE平分∠BOD
∴∠BOE=∠DOE=180°-x°
∵![]() 平分
平分![]()
∴∠COF=∠EOF=![]()
∴∠BOF=∠EOF-∠BOE=![]()
∵![]()
即![]()
解得:![]()
∴∠COE=130°,∠BOE=∠DOE=180°-130°=50°,
∴∠AOC=∠BOD=2∠DOE=100°,
故∠AOC=100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
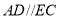 .
.(1)若
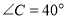 ,
,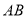 平分
平分 ,求
,求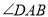 的度数;
的度数;(2)若
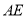 平分
平分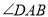 ,
, 平分
平分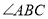 .
.①求证
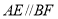 ;
;②将结论
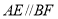 与条件
与条件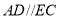 互换位置,其他条件不变,组成一个新的命题,判断该命题的真假,并写出证明过程.
互换位置,其他条件不变,组成一个新的命题,判断该命题的真假,并写出证明过程.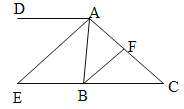
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,每个小正方形的边长均为
,每个小正方形的边长均为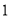 ,阴影部分是一个正方形.
,阴影部分是一个正方形.(1)阴影部分的面积是__________,边长是____________;
(2)写出不大于阴影正方形边长的所有正整数;
(3)
 为阴影正方形边长的小数部分,
为阴影正方形边长的小数部分, 为
为 的整数部分,求
的整数部分,求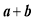 的值.
的值.
-
科目: 来源: 题型:
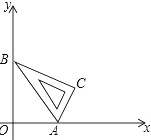
查看答案和解析>>【题目】如图,将含有30°角的直角三角板ABC放入平面直角坐标系,顶点A,B分别落在x、y轴的正半轴上,∠OAB=60°,点A的坐标为(1,0),将三角板ABC沿x轴向右作无滑动的滚动(先绕点A按顺时针方向旋转60°,再绕点C按顺时针方向旋转90°,…)当点B第一次落在x轴上时,则点B运动的路径与坐标轴围成的图形面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.

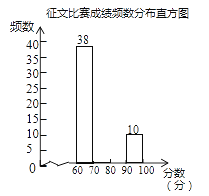
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课上老师提出一个问题:“如图,已知
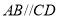 ,
,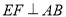 于点
于点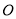 ,
,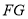 交
交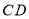 于点
于点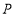 ,当
,当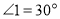 时,求
时,求 的度数.”
的度数.”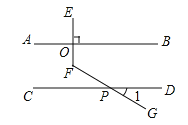
甲、乙、丙三位同学用不同的方法添加辅助线解决问题如图1,图2,图3所示.
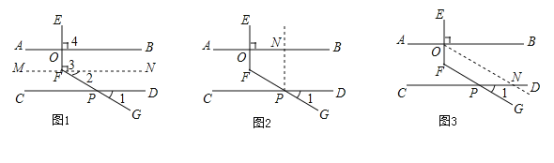
(1)补全甲同学的分析思路.
辅助线:过点
 作
作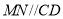 .
.分析思路:
①欲求∠EFG的度数,由图可知只需转化为求________和___________的度数之和;
②由辅助线作图可知
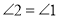 ;
;③由
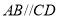 ,
,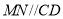 推出_________________,由此可推出
推出_________________,由此可推出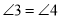 ;
;④由已知
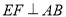 ,可得
,可得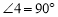 ,所以可得
,所以可得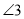 的度数,从而可求
的度数,从而可求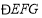 的度数.
的度数.(2)请你根据乙同学所画的辅助线,补全求解过程.
解:过
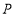 作___________________,交
作___________________,交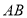 于点
于点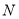 .
. ___________________________
___________________________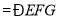 (两直线平行,同位角相等).
(两直线平行,同位角相等).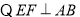 ,
,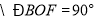 ,
,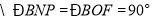 (_______________________).
(_______________________).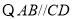 .
.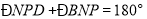 (____________________________),
(____________________________),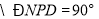 ,
,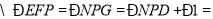 _______________________.
_______________________.(3)请你根据丙同学所画的辅助线,求
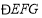 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中,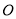 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点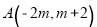 在
在 轴上,点
轴上,点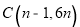 在
在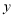 轴上,点
轴上,点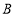 在第一象限内,点
在第一象限内,点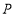 从原点出发,以每秒
从原点出发,以每秒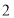 个单位长度的速度沿着
个单位长度的速度沿着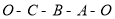 的路线移动(即沿着长方形的边移动一周).
的路线移动(即沿着长方形的边移动一周).(1)分别求出
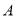 ,
,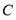 两点的坐标;
两点的坐标;(2)当点
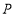 移动了
移动了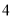 秒时,求出点
秒时,求出点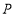 的坐标;
的坐标;(3)在移动过程中,当三角形
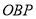 的面积是
的面积是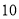 时,求满足条件的点
时,求满足条件的点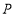 的坐标及相应的点
的坐标及相应的点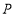 移动的时间.
移动的时间.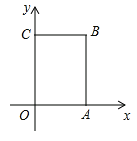
相关试题

