【题目】如图,在△ABD中,AB=AD, 将△ABD沿BD翻折,使点A翻折到点C. E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE.
(1)依题意补全图形;
(2)判断∠DFC与∠BAE的大小关系并加以证明;
(3)若∠BAD=120°,AB=2,取AD的中点G,连结EG,求EA+EG的最小值.


参考答案:
【答案】(1)见解析;(2)判断:∠DFC=∠BAE. 证明见解析;(3)EA+EG的最小值为![]() .
.
【解析】(1)将△ABD沿BD翻折,使点A翻折到点C.E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE,据此画图即可;(2)根据△ABE≌△CBE(SAS),可得∠BAE=∠BCE.再根据AD∥BC,可得∠DFC=∠BCE,进而得出∠DFC=∠BAE;(3)连接CG,AC,根据EC+EG≥CG可知,CG长就是EA+EG的最小值,根据△ACD为边长为2的等边三角形,G为AD的中点,运用勾股定理即可得出CG=![]() ,进而得到EA+EG的最小值.
,进而得到EA+EG的最小值.
(1)补全图形如下:
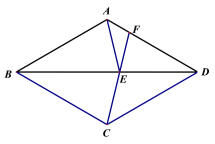
(2)判断:∠DFC=∠BAE.
证明:∵将△ABD沿BD翻折,使点A翻折到点C.
∴BC=BA=DA=CD. ∴四边形ABCD为菱形.
∴∠ABD=∠CBD,AD∥BC.
又∵BE=BE,∴△ABE≌△CBE(SAS).
∴∠BAE=∠BCE.
∵AD∥BC,
∴∠DFC=∠BCE.
∴∠DFC=∠BAE.
(3)连CG, AC.
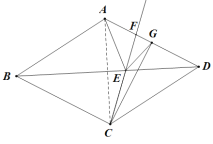
由![]() 轴对称可知,EA+EG=EC+EG,
轴对称可知,EA+EG=EC+EG,
CG长就是EA+EG的最小值.
∵∠BAD=120°,四边形ABCD为菱形,
∴∠CAD=60°.
∴△ACD为边长为2的等边三角形.
可求得CG=![]() .
.
∴EA+EG的最小值为![]() .
.
-
科目: 来源: 题型:
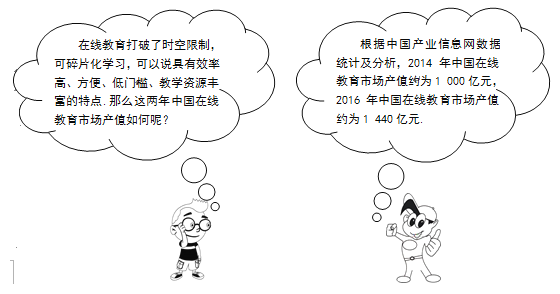
查看答案和解析>>【题目】“在线教育”指的是通过应用信息科技和互联网技术进行内容传播和快速学习的方法.“互联网+”时代,中国的在线教育得到迅猛发展. 请根据下面张老师与记者的对话内容,求2014年到2016年中国在线教育市场产值的年平均增长率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.
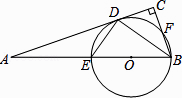
(1)求证:AC是⊙O的切线;
(2)当BC=2,cos∠ABC= 时,求⊙O的半径.
时,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的解题过程并回答问题.
解方程:
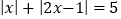 .
.解:①当
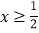 时,原方程可化为
时,原方程可化为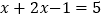 ,解得
,解得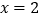 .经检验,符合题意;
.经检验,符合题意;②当
 时,原方程可化为
时,原方程可化为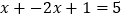 ,解得
,解得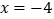 .经检验,x的值不合题意,舍去;
.经检验,x的值不合题意,舍去;③当
 时,原方程可化为
时,原方程可化为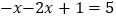 ,解得
,解得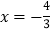 音.经检验,符合题意.
音.经检验,符合题意.所以原方程的解是
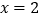 或
或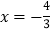 .
.(1)根据上面的解题过程,求方程
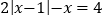 的解;
的解;(2)根据上面的解题过程,求方程
 的解;
的解;(3)方程
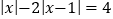 解.(填“有”或“无”)
解.(填“有”或“无”) -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距64 km,甲从A地出发,每小时行14 km,乙从B地出发,每小时行18 km.
(1)若两人同时出发相向而行,则需经过几小时两人相遇?
(2)若两人同时出发相向而行,则需经过几小时两人相距16 km?
(3)若甲在前,乙在后,两人同时同向而行,则几小时后乙超过甲10 km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
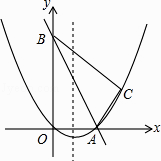
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品
篮球
排球
羽毛球拍
单价(元)
50
40
25
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)
相关试题

