【题目】A、B两地相距64 km,甲从A地出发,每小时行14 km,乙从B地出发,每小时行18 km.
(1)若两人同时出发相向而行,则需经过几小时两人相遇?
(2)若两人同时出发相向而行,则需经过几小时两人相距16 km?
(3)若甲在前,乙在后,两人同时同向而行,则几小时后乙超过甲10 km?
参考答案:
【答案】(1) 2小时;(2) 1.5小时或2.5小时;(3) 18.5小时.
【解析】
(1)如果两人同时出发相向而行,那么是相遇问题,设两人同时出发相向而行,需经过x小时两人相遇,即x小时他们共同走完64千米,由此可以列出方程解决问题;
(2) 此小题有两种情况:①还没有相遇他们相距16千米;②已经相遇他们相距16千米.但都可以利用相遇问题解决;
(3) 若甲在前,乙在后,两人同时同向而行,此时是追及问题,设![]() 小时后乙超过甲10千米,那么
小时后乙超过甲10千米,那么![]() 小时甲走了14
小时甲走了14![]() 千米,乙走了18
千米,乙走了18![]() 千米,然后利用已知条件即可列出方程解决问题.
千米,然后利用已知条件即可列出方程解决问题.
解:(1)设两人同时出发相向而行,需经过x小时两人相遇,
![]()
![]()
答:两人同时出发相向而行,需经过2小时两人相遇;
(2)设两人同时出发相向而行,需y小时两人相距16千米,
①当两人没有相遇他们相距16千米,
![]()
![]()
②当两人已经相遇他们相距16千米,
![]()
![]()
答:若两人同时出发相向而行,则需1.5或2.5小时两人相距16千米;
(3)设甲在前,乙在后,两人同时同向而行,则z小时后乙超过甲10千米,
![]()
![]()
答:若甲在前,乙在后,两人同时同向而行,则18.5小时后乙超过甲10千米.
故答案是:(1) 2小时;(2) 1.5小时或2.5小时;(3) 18.5小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.
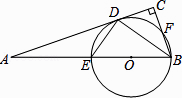
(1)求证:AC是⊙O的切线;
(2)当BC=2,cos∠ABC= 时,求⊙O的半径.
时,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的解题过程并回答问题.
解方程:
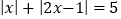 .
.解:①当
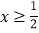 时,原方程可化为
时,原方程可化为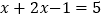 ,解得
,解得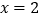 .经检验,符合题意;
.经检验,符合题意;②当
 时,原方程可化为
时,原方程可化为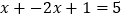 ,解得
,解得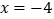 .经检验,x的值不合题意,舍去;
.经检验,x的值不合题意,舍去;③当
 时,原方程可化为
时,原方程可化为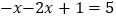 ,解得
,解得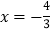 音.经检验,符合题意.
音.经检验,符合题意.所以原方程的解是
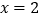 或
或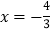 .
.(1)根据上面的解题过程,求方程
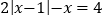 的解;
的解;(2)根据上面的解题过程,求方程
 的解;
的解;(3)方程
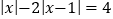 解.(填“有”或“无”)
解.(填“有”或“无”) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD中,AB=AD, 将△ABD沿BD翻折,使点A翻折到点C. E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE.
(1)依题意补全图形;
(2)判断∠DFC与∠BAE的大小关系并加以证明;
(3)若∠BAD=120°,AB=2,取AD的中点G,连结EG,求EA+EG的最小值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
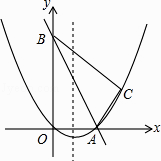
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品
篮球
排球
羽毛球拍
单价(元)
50
40
25
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
相关试题

